KPSS test is a statistical test to check for stationarity of a series around a deterministic trend. Like ADF test, the KPSS test is also commonly used to analyse the stationarity of a series. However, it has couple of key differences compared to the ADF test in function and in practical usage. Therefore, is not safe to just use them interchangeably. We’ll discuss this detail with simplified examples.
1. Introduction
The KPSS test, short for, Kwiatkowski-Phillips-Schmidt-Shin (KPSS), is a type of Unit root test that tests for the stationarity of a given series around a deterministic trend.
In other words, the test is somewhat similar in spirit with the ADF test.
A common misconception, however, is that it can be used interchangeably with the ADF test. This can lead to misinterpretations about the stationarity, which can easily go undetected causing more problems down the line.
In this article, you will see how to implement KPSS test in python, how it is different from ADF test and when and what all things you need to take care when implementing a KPSS test.
Let’s begin.
2. How to implement KPSS test
In python, the statsmodel package provides a convenient implementation of the KPSS test.
A key difference from ADF test is the null hypothesis of the KPSS test is that the series is stationary.
So practically, the interpretaion of p-value is just the opposite to each other.
That is, if p-value is < signif level (say 0.05), then the series is non-stationary. Whereas in ADF test, it would mean the tested series is stationary.
Alright let’s implement the test on the ‘daily temperatures’ dataset.
This dataset contains the minimum daily temperature of the Melbourne city from 1981 to 1990. Let’s first read it in pandas and plot it.
# Import data
import pandas as pd
import numpy as np
path = 'https://raw.githubusercontent.com/selva86/datasets/master/daily-min-temperatures.csv'
df = pd.read_csv(path, parse_dates=['Date'], index_col='Date')
df.plot(title='Daily Temperatures', figsize=(14,8), legend=None);
To implement the KPSS test, we’ll use the kpss function from the statsmodel. The code below implements the test and prints out the returned outputs and interpretation from the result.
# KPSS test
from statsmodels.tsa.stattools import kpss
def kpss_test(series, **kw):
statistic, p_value, n_lags, critical_values = kpss(series, **kw)
# Format Output
print(f'KPSS Statistic: {statistic}')
print(f'p-value: {p_value}')
print(f'num lags: {n_lags}')
print('Critial Values:')
for key, value in critical_values.items():
print(f' {key} : {value}')
print(f'Result: The series is {"not " if p_value < 0.05 else ""}stationary')
kpss_test(series)
Result:
KPSS Statistic: 0.5488001951803195
p-value: 0.030675631716144246
num lags: 10
Critial Values:
10% : 0.347
5% : 0.463
2.5% : 0.574
1% : 0.739
Result: The series is not stationary
3. How to interpret KPSS test results
The output of the KPSS test contains 4 things:
- The KPSS statistic
- p-value
- Number of lags used by the test
- Critical values
The p-value reported by the test is the probability score based on which you can decide whether to reject the null hypothesis or not. If the p-value is less than a predefined alpha level (typically 0.05), we reject the null hypothesis.
The KPSS statistic is the actual test statistic that is computed while performing the test. For more information no the formula, the references mentioned at the end should help.
In order to reject the null hypothesis, the test statistic should be greater than the provided critical values. If it is in fact higher than the target critical value, then that should automatically reflect in a low p-value.
That is, if the p-value is less than 0.05, the kpss statistic will be greater than the 5% critical value.
Finally, the number of lags reported is the number of lags of the series that was actually used by the model equation of the kpss test. By default, the statsmodels kpss() uses the ‘legacy’ method. In legacy method, int(12 * (n / 100)**(1 / 4)) number of lags is included, where n is the length of the series.
4. How is KPSS test different from ADF test
A major difference between KPSS and ADF tests is the capability of the KPSS test to check for stationarity in the ‘presence of a deterministic trend’.
If you go back and read the definition of the KPSS test, it tests for stationarity of the series around a ‘deterministic trend’.
What that effectively means to us is, the test may not necessarily reject the null hypothesis (that the series is stationary) even if a series is steadily increasing or decreasing.
But what is a ‘deterministic trend’?
The word ‘deterministic’ implies the slope of the trend in the series does not change permanently. That is, even if the series goes through a shock, it tends to regain its original path.
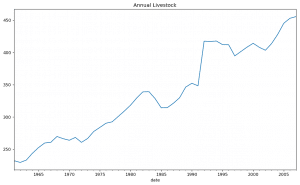
Well, let’s test out the stationarity of the ‘livestock‘ time series from the fpp R package. Let me import the data and visualize first.
import pandas as pd
import numpy as np
path = 'https://raw.githubusercontent.com/selva86/datasets/master/livestock.csv'
df = pd.read_csv(path, parse_dates=['date'], index_col='date')
fig, axes = plt.subplots(1,1, dpi=120)
df.plot(title='Annual Livestock', figsize=(12,7), legend=None, ax=axes);
There appears to be a steady increasing trend overall. So, you could expect that this series is stationary around the trend.
Lets see.
Applying the KPSS test . .
# KPSS test: stationarity around a trend
series = df.loc[:, 'value'].values
kpss_test(series)
Result:
KPSS Statistic: 0.5488001951803195
p-value: 0.030675631716144246
num lags: 10
Critial Values:
10% : 0.347
5% : 0.463
2.5% : 0.574
1% : 0.739
Result: The series is not stationary
The test says the p-value is significant (with p_value < 0.05) and hence, you can reject the null hypothesis (series is stationary) and derive that the series is NOT stationary.
But we thought the KPSS should not have rejected the null, because of the ‘stationarity around a deterministic trend’. Yes?
Well, that’s probably because we used the default option of the KPSS test.
By default, it tests for stationarity around a ‘mean’ only.
5. KPSS test around a deterministic trend
In KPSS test, to turn ON the stationarity testing around a trend, you need to explicitly pass the regression='ct' parameter to the kpss.
kpss_test(series, regression='ct')
KPSS Statistic: 0.11743798430485435
p-value: 0.1
num lags: 10
Critial Values:
10% : 0.119
5% : 0.146
2.5% : 0.176
1% : 0.216
Result: The series is stationary
Now clearly, the p-value is so high that you cannot reject the null hypothesis. So the series is stationary.
For the curious, What happens if you test the same series using the Augmented Dickey Fuller (ADF) test?
Let’s find out
# ADF test on random numbers
from statsmodels.tsa.stattools import adfuller
def adf_test(series):
result = adfuller(series, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
print('Critial Values:')
print(f' {key}, {value}')
series = df.loc[:, 'value'].values
adf_test(series)
ADF Statistic: -0.2383837252990996
p-value: 0.9337890318823667
Critial Values:
1%, -3.5812576580093696
Critial Values:
5%, -2.9267849124681518
Critial Values:
10%, -2.6015409829867675
Unlike KPSS test, the null hypothesis in ADF test is the series is not stationary.
Since p-value is well above the 0.05 alpha level, you cannot reject the null hypothesis. So the series is NOT stationary according to ADF test, which is actually expected.
6. Conclusion
So overall what this means to us is, if a series is stationary according to the KPSS test by setting regression='ct' and is not stationary according to the ADF test, it means the series is stationary around a deterministic trend and so is fairly easy to model this series and produce fairly accurate forecasts.
With that we have covered the core intuition behind KPSS test with practical examples. If you have any questions, please leave a line in the comments.
Thanks for joining and see you in the next one.
7. References
Kwiatkowski, D.; Phillips, P. C. B.; Schmidt, P.; Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root. Journal of Econometrics, 54 (1-3): 159-178.