Measures of Dispersion – Unlocking the Variability Diving Deep into Measures of Dispersion

Dive deep into the world of statistics and measures of dispersion, from understanding its essence to its practical application using Python.

In this Blog post we will learn:

1. What is Dispersion in Statistics?
2. Advantages and Applications of Measures of Dispersion:
3. Types of Measures of Dispersion
   3.1. Absolute Measure of Dispersion
   3.2. Relative Measure of Dispersion
4. Different ways to visualize the measures of dispersion
5. Conclusion

1. What is Dispersion in Statistics?

Dispersion in statistics refers to the extent to which a set of data is spread out. While central tendency (like mean, median, and mode) gives us a central value of the data set, dispersion gives us an idea of how spread out the data points are around this central value. A set of data can have the same mean or median but can vary significantly in their levels of dispersion.

2. Advantages and Applications of Measures of Dispersion:

1. Better Understanding: Dispersion measures give a more comprehensive picture of the data. Knowing only the average doesn’t tell us about the variability or consistency of data.

2. Comparing Variability: By understanding dispersion, we can compare the variability of two or more sets of data.

3. Predictive Analysis: In fields like finance and stock markets, measures of dispersion such as variance and standard deviation help in assessing risks.

4. Quality Control: In manufacturing, understanding dispersion helps in ensuring the consistency of products.

3. Types of Measures of Dispersion

There are two main categories:

1. Absolute Measure of Dispersion: These measures give the dispersion in the same units as the original data. They are independent of the unit of measurement.

   Absolute dispersion methods include:

   • Range
   • Variance and Standard Deviation
   • Quartile Deviation

1. Relative Measure of Dispersion: These measures are dimensionless and are usually expressed in percentage form. They help in comparing the dispersion of two or more sets of data.

   Relative dispersion methods include:

   • Coefficient of Range
   • Coefficient of Variation (CV)
   • Coefficient of Quartile Deviation

3.1. Absolute Measure of Dispersion

1. Range:
It is the simplest measure of dispersion.
– Formula:
Range = Maximum value – Minimum value

- **Where:**  
  - Maximum value is the largest value in the dataset.
  - Minimum value is the smallest value in the dataset.

• Example:
  For data set {5, 12, 18, 23}, Range = 23 – 5 = 18

data = [5, 12, 18, 23]
range_value = max(data) - min(data)
print("Range:", range_value)  # Output: Range: 18

Range: 18

2. Variance and Standard Deviation:
For ungrouped data, variance is the average of the squared differences from the Mean.

• Variance (σ^2):
  $ \sigma^2 = \frac{\sum (X_i – \bar{X})^2}{N} $
  • Where:
    • $X_i$ represents each individual data point.
    • $\bar{X}$ represents the mean of the data.
    • $N$ represents the total number of data points.
      
• Standard Deviation (σ):
  $ \sigma = \sqrt{\sigma^2} $
  • Where:
    • $\sigma^2$ represents the variance.

• Example:
  For data set {2, 4, 4, 4, 5, 5, 7, 9}, Variance = 4.571 and Standard Deviation = 2.138

import statistics
data = [2, 4, 4, 4, 5, 5, 7, 9]
variance = statistics.variance(data)
std_dev = statistics.stdev(data)
print("Variance:", variance)  # Output: Variance: 4.571428571428571
print("Standard Deviation:", std_dev)  # Output: Standard Deviation: 2.138089935299395

Variance: 4.571428571428571
Standard Deviation: 2.138089935299395

3. Quartile Deviation (or Semi-Interquartile Range):
It is half the difference between the first and the third quartile.
– Formula:
$ QD = \frac{Q3 – Q1}{2} $

• Where:
  • $Q1$ represents the first quartile.
  • $Q3$ represents the third quartile.

import numpy as np
data = [5, 7, 8, 9, 10, 12, 14, 16, 18]
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
QD = (Q3 - Q1) / 2
print("Quartile Deviation:", QD) 

Quartile Deviation: 3.0

3.2. Relative Measure of Dispersion

1. Coefficient of Range:
It is the ratio of the range to the sum of the maximum and minimum values.
– Formula:
$ CR = \frac{Range}{Maximum + Minimum} $

- **Where:**  
  - Range is the difference between the maximum and minimum values.
  - Maximum value is the largest value in the dataset.
  - Minimum value is the smallest value in the dataset.

data = [5, 12, 18, 23]
range_value = max(data) - min(data)
CR = range_value / (max(data) + min(data))
print("Coefficient of Range:", CR) 

Coefficient of Range: 0.6428571428571429

2. Coefficient of Variation (CV):
It is the ratio of the standard deviation to the mean expressed as a percentage.
– Formula:
$ CV = \frac{σ}{\bar{X}} \times 100\% $

- **Where:**  
  - $\sigma$ represents the standard deviation.
  - $\bar{X}$ represents the mean of the data.

• Example:
  If the standard deviation of a data set is 5 and the mean is 20, CV = 25%.

data = [10, 20, 30, 40, 50]
mean = statistics.mean(data)
std_dev = statistics.stdev(data)
CV = (std_dev/mean) * 100
print("Coefficient of Variation:", CV, "%")  # Output: Coefficient of Variation: 44.7213595499958 %

Coefficient of Variation: 52.70462766947299 %

3. Coefficient of Quartile Deviation:
It is the ratio of the quartile deviation to the average of the first and third quartiles.
– Formula:
$ CQD = \frac{QD}{\frac{Q1 + Q3}{2}} $

- **Where:**  
  - $QD$ represents the quartile deviation.
  - $Q1$ represents the first quartile.
  - $Q3$ represents the third quartile.

data = [5, 7, 8, 9, 10, 12, 14, 16, 18]

Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
QD = (Q3 - Q1) / 2
CQD = QD / ((Q1 + Q3) / 2)

print(f"Coefficient of Quartile Deviation: {CQD:.2f}")

Coefficient of Quartile Deviation: 0.27

4. Different ways to visualize the measures of dispersion

Visualizing measures of dispersion can help in understanding the spread of data. Python, particularly with libraries like Matplotlib and Seaborn, provides an array of visualization options to display measures of dispersion.

Here are some common ways:

1. Box Plot (Box-and-Whisker Plot):

• It shows the median, quartiles, and potential outliers in the dataset.
• Dispersion is represented by the interquartile range (IQR) and the whiskers of the plot.

import seaborn as sns
data = [5, 7, 8, 8, 9, 10, 12, 12, 14, 15, 16, 18]
sns.boxplot(data=data)

2. Histogram:

• It showcases the distribution of data.
• The width of the bars indicates the range of the data, while the height of the bars indicates the frequency.

import matplotlib.pyplot as plt
import numpy as np

# Set seed for reproducibility
np.random.seed(42)

# Generate 1000 random data points
data = np.random.randn(1000)

plt.hist(data, bins=10, edgecolor="k", alpha=0.7)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('Histogram of Data')
plt.show()

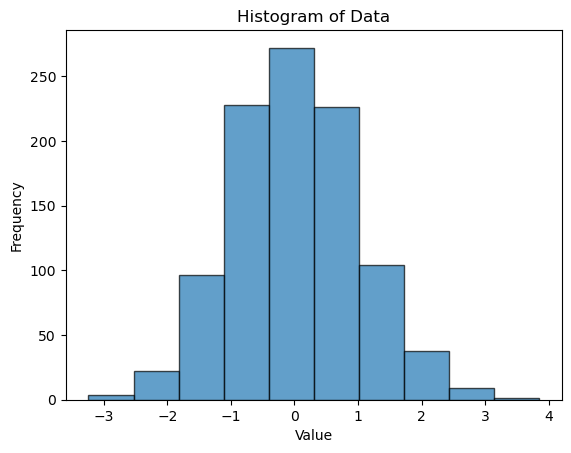
3. Variance and Standard Deviation:

Using a line plot or scatter plot, you can highlight the mean and then showcase the standard deviation away from the mean.

# Set seed for reproducibility
np.random.seed(42)

# Generate 1000 random data points
data = np.random.randn(1000)

mean = sum(data)/len(data)
std_dev = (sum([(x-mean)**2 for x in data]) / len(data))**0.5

plt.axvline(mean, color='red', linestyle='dashed', linewidth=1, label=f'Mean: {mean}')
plt.axvline(mean+std_dev, color='blue', linestyle='dashed', linewidth=1, label=f'Standard Deviation: {std_dev}')
plt.axvline(mean-std_dev, color='blue', linestyle='dashed', linewidth=1)

plt.legend(loc="upper right")
plt.hist(data, bins=10, edgecolor="k", alpha=0.7)
plt.show()

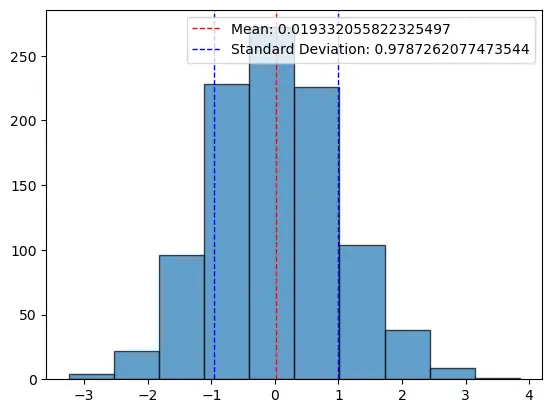
4. Violin Plot:

• It’s a combination of a box plot and a kernel density estimation.
• This plot showcases the probability density of the data at different values.

sns.violinplot(data=data)

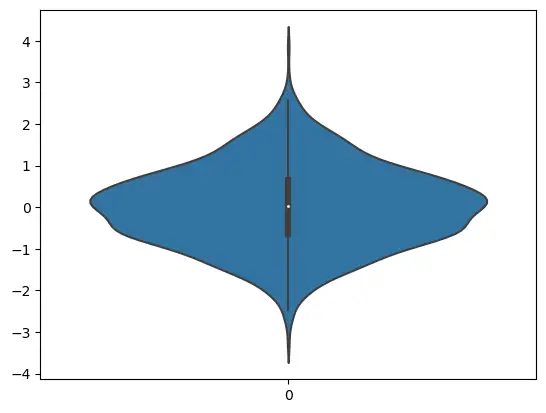
5. Standard Deviation Bars:

Overlaying the standard deviation on bar charts to showcase the variability of multiple datasets.

categories = ['A', 'B', 'C']
values = [50, 60, 55]
std_devs = [5, 8, 3]

plt.bar(categories, values, yerr=std_devs, capsize=10, color='lightblue', edgecolor='k')
plt.ylabel('Value')
plt.title('Bar Chart with Standard Deviation Bars')
plt.show()

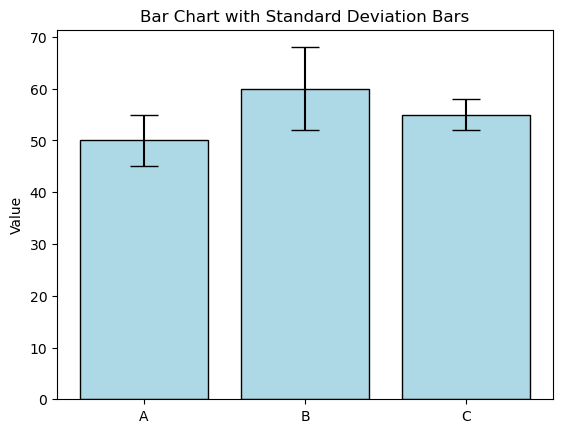
5. Conclusion

Measures of dispersion not only provide a holistic understanding of datasets but, when leveraged correctly, can lead to more nuanced insights and better decision-making. With Python, these measures are just a few lines of code away, offering a powerful blend of theory and application for statisticians.