Statistics offers a vast array of principles and theorems that are foundational to how we understand data. Among them, the Central Limit Theorem (CLT) stands as one of the most important.
Let’s dive deeper into the concept, ensuring that all points are covered and clarified.

In this blog post we will learn:
- Simple Explanation of the Central Limit Theorem (CLT)
- Concepts to Learn Before the Central Limit Theorem:
- What is the Central Limit Theorem?
3.1. Why is the Central Limit Theorem Important?
3.2. Assumptions and Requirements
3.3. Applications of Central Limit Theorem
3.4. Limitations of Central Limit Theorem - Central Limit Theorem in Action
4.1. Demonstrate the Central Limit Theorem (CLT) in action usign Python - Conclusion
1. Simple Explanation of the Central Limit Theorem (CLT)
Imagine you’re in a town where people have all sorts of heights, from very short to very tall.
Let’s say, you pick few people at random, say 5 nos, and calculate their average height, you might get a number. Maybe they’re all tall, maybe they’re all short, or maybe they’re a mix.
But if you do this over and over again – pick a group, calculate the average, then pick another group – and then you plot a graph of all those averages, a surprising thing happens: Your graph starts to look like a bell curve (called a normal distribution), no matter the original distribution of heights in the town.
The more people you pick each time (larger sample size), the closer this bell curve will be to a perfect shape. The CLT tells us this phenomenon isn’t just true for heights, but for a lot of things.
2. Concepts to Learn Before the Central Limit Theorem:
- Population vs. Sample: A population includes every member of a specified group. A sample is a subset of that group. For instance, all residents of a town would be the population, whereas a group of 100 residents selected from that town would be a sample.
-
Mean: The average value. For instance, the average height of a group of people.
-
Standard Deviation: A measure of how spread out the numbers in a data set are. If everyone in a group is about the same height, the standard deviation is small. If their heights are all over the place, the standard deviation is large.
-
Probability: The measure of the likelihood that an event will occur.
-
Probability Distribution: A mathematical function that provides the probabilities of occurrence of different possible outcomes. For example, in a dice throw, there’s a 1/6 chance for each number from 1 to 6.
-
Sampling Distribution: The probability distribution of a statistic (like the mean) based on many samples from the same population.
-
Normal Distribution (or Bell Curve): A specific probability distribution that is symmetric and has a bell-shaped curve. Many natural phenomena follow this distribution.
3. What is the Central Limit Theorem?
In simple terms, the Central Limit Theorem (CLT) states that regardless of the original distribution of the population, the sampling distribution of the sample mean approaches a normal distribution as the sample size increases. This is true when the sample size is sufficiently large, typically considered as n > 30.
3.1. Why is the Central Limit Theorem Important?
The central limit theorem is considered helpful for various reasons:
- A Foundational Principle in Inferential Statistics: CLT forms the foundation for many statistical procedures and tests, especially when the original data doesn’t follow a normal distribution.
-
To draw inferences: By knowing that the sampling distribution will be approximately normal, we can use the properties of a normal distribution to make inferences about population parameters.
-
Applicability: As many natural phenomena are described by non-normal distributions, the CLT provides a way to make robust inferences based on the normality of sample means.
3.2. Assumptions and Requirements
There are few assumptions you need to consider then applying the the central limit theorem.
- Random Sampling: Samples should be drawn randomly from the population.
-
Independence: The sampled observations should be independent. This means that the occurrence of one event does not affect the probability of the other. This is often met if the sample is less than 10% of the population.
-
Sample Size: Typically, a sample size above 30 is considered sufficient for the CLT to hold, though for largely skewed data, a larger sample might be necessary.
3.3. Applications of Central Limit Theorem
Central limit theorem is a foundational concept in statistics and is helpful in various other concepts / techniques as well:
- Confidence Intervals: CLT allows us to create confidence intervals around our sample mean for the population mean, even for non-normally distributed data.
-
Hypothesis Testing: Many tests, like the t-test, assume that data is normally distributed. Even if the original data isn’t normal, CLT ensures the sampling distribution is, allowing us to use such tests.
-
Quality Control: In industries, especially manufacturing, the CLT is used to understand variations and bring products within quality specifications.
3.4. Limitations of Central Limit Theorem
While the Central Limit Theorem is widely applicable, it is not a magic bullet. For very skewed data or data with heavy tails, a larger sample size might be required. Also, it doesn’t apply to median or mode, only the mean.
4. Central Limit Theorem in Action
Population Distribution: Imagine a dice, whose outcomes (1, 2, 3, 4, 5, or 6) do not form a normal distribution. If we were to plot the probabilities, we would get a flat distribution since each outcome has an equal probability.
Sample Distribution: Let’s consider taking a sample of 2 dice rolls and calculating the average. The possible means range from 1 (if both dice show 1) to 6 (if both show 6). If you were to plot the frequencies of these sample means, the resulting shape would start to look a bit like a bell curve, though not perfectly normal.
Increasing Sample Size: As the sample size increases, say 10 dice rolls, the shape becomes more and more like a perfect bell curve. This is the magic of the Central Limit Theorem in action!
4.1. Demonstrate the Central Limit Theorem (CLT) in action usign Python
Here’s what we’ll do:
- Start with importing sampe data.
- Randomly sample from this distribution multiple times, taking the mean each time.
- Plot the resulting means to show they follow a normal distribution.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
# Load the Iris dataset
url = 'https://raw.githubusercontent.com/selva86/datasets/master/Iris.csv'
iris = pd.read_csv(url)
iris.head()
| Id | SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | Species | |
|---|---|---|---|---|---|---|
| 0 | 1 | 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 1 | 2 | 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| 2 | 3 | 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa |
| 3 | 4 | 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa |
| 4 | 5 | 5.0 | 3.6 | 1.4 | 0.2 | Iris-setosa |
# Let's use the sepal length for our demonstration
data = iris['SepalLengthCm'].values
# Sample from the data and store the means
sample_means = []
num_samples = 1000
sample_size = 30 # You can play with this number. As it increases, the result becomes more "normal".
for _ in range(num_samples):
sample = np.random.choice(data, sample_size) # This randomly picks 'sample_size' data points from data
sample_means.append(np.mean(sample))
# Plot the sample means
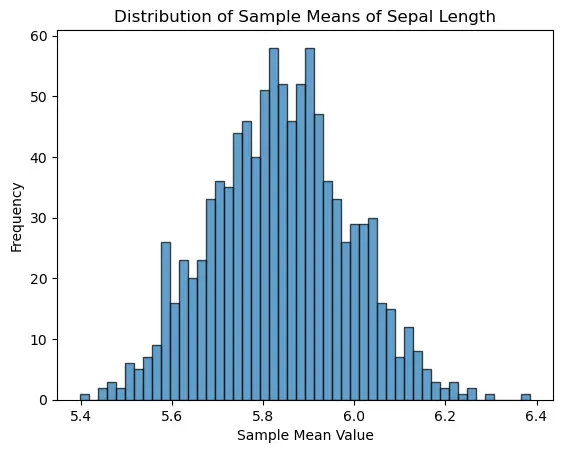
plt.hist(sample_means, bins=50, edgecolor='k', alpha=0.7)
plt.title('Distribution of Sample Means of Sepal Length')
plt.xlabel('Sample Mean Value')
plt.ylabel('Frequency')
plt.show()
5. Conclusion
The Central Limit Theorem is one of the shining stars in the world of statistics, allowing us to make robust inferences about populations based on sample data.
It bridges the gap between real-world non-normal data and the theoretical world of normally distributed data. As budding data enthusiasts, understanding and harnessing the power of the CLT can significantly enhance our data analysis toolkit.





