Continuous Frequency Distributions – Understanding Continuous Frequency Distributions and the Probability Density Function (PDF)

Lets deep dive into the world of statistics to understand the mysteries of continuous frequency distributions and the probability density function (PDF). By the end of this post, you’ll have a clearer understanding of these foundational concepts and their significance in the statistics.

In this Blog post we will learn:

1. Continuous Frequency Distributions:
2. Constructing the Frequency Distribution
3. Probability Density Function (PDF)
   3.1. Estimating Density
4. Probability Density Function (PDF) Estimation:
5. Visualizing Probability Distributions using Python
6. Types of Continuous Frequency Distributions:
   6.1. Normal (Gaussian) Distribution
   6.2. Uniform Distribution
   6.3. Exponential Distribution
   6.4. Gamma Distribution
   6.5. Beta Distribution
   6.6. Chi-Squared Distribution
   6.7. Weibull Distribution
   6.8. Log-Normal Distribution
7. Conclusion:

1. Continuous Frequency Distributions:

The term “distribution” refers to the way in which a set of data points are spread or scattered across a range of values. When we talk about continuous frequency distributions, we’re looking at data that can take on any value within a specified range. This is in contrast to discrete data, which can only take on specific, separate values (like the number of pets someone has, which can only be whole numbers).

Imagine measuring the height of every person in a city. Since height can vary by very small amounts, you have a continuous data set. In a continuous frequency distribution, instead of listing each individual height, you’d group the heights into intervals (like 5’0″ to 5’1″, 5’1″ to 5’2″, and so on)..

Continuous variables, such as height, weight, or expenditure, can take any value within a given range. When we collect data on such variables, one of the ways to summarize and visualize this data is through a continuous frequency distribution.

A continuous frequency distribution groups data into intervals and tells us how many data points fall into each interval.

Let’s consider sample data on monthly expenditure on groceries of 50 families in a neighborhood (in USD):

# Sample data
expenditure = [105, 120, 130, 125, 140, 110, 135, 145, 125, 115, 140, 150, 
               120, 155, 135, 130, 125, 155, 145, 135, 110, 145, 160, 165, 
               130, 125, 150, 155, 165, 160, 135, 140, 120, 130, 145, 150, 
               165, 155, 160, 135, 120, 110, 155, 160, 165, 130, 145, 140, 135, 125] # truncated for brevity

2. Constructing the Frequency Distribution

1. Determine the Range:
   • Lowest value = 105
   • Highest value = 165
   • Range = 60
2. Choose Intervals:
   • We chose 6 intervals with a width of 10.
3. Count Observations:

Interval	Frequency
105-115	4
115-125	3
125-135	8
135-145	10
145-155	9
155-165	6

3. Probability Density Function (PDF)

The Probability Density Function (PDF) provides a description of the probability of a continuous random variable taking on a particular value. For a continuous random variable $X$, the probability that $X$ takes on any specific value $x$ is technically 0. Instead, we often look at the probability that $X$ falls within a specific interval.

3.1. Estimating Density

The density of a histogram bar is a measure that allows the area of the bar to represent the proportion of data points in that interval. The formula for density is:

$ \text{Density} = \frac{f}{N \times w} $

Where:

• $ f $ is the frequency of the interval
• $ N $ is the total number of observations
• $ w $ is the width of the interval

4. Probability Density Function (PDF) Estimation:

Total number of observations = 50

Interval width = 10

1. For 105-115 : $ \text{Density} = \frac{4}{50 \times 10} $ = 0.008

2. For 115-125 : $ \text{Density} = \frac{3}{50 \times 10} $ = 0.006

3. For 125-135 : $ \text{Density} = \frac{8}{50 \times 10} $ = 0.016

4. For 135-145 : $ \text{Density} = \frac{10}{50 \times 10} $ = 0.020

5. For 145-155 : $ \text{Density} = \frac{9}{50 \times 10} $ = 0.018

6. For 155-165 : $ \text{Density} = \frac{6}{50 \times 10} $ = 0.012

Using this formula, we calculate the densities for our intervals:

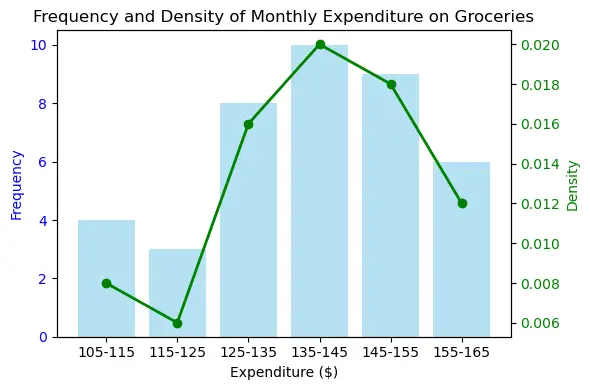
Interval	Frequency	Density
105-115	4	0.008
115-125	3	0.006
125-135	8	0.016
135-145	10	0.020
145-155	9	0.018
155-165	6	0.012

5. Visualizing Probability Distributions using Python

Visualizing these distributions can be insightful. Let’s see how we can visualize each of the mentioned distributions using Python’s matplotlib and numpy libraries. If not already installed, you can install these libraries using pip

To visualize the data, we’ll plot both the frequency and density using Python’s popular matplotlib library:

pip install matplotlib numpy

# Additionally, we'll use the scipy.stats module for some distributions

pip install scipy

import matplotlib.pyplot as plt

# Sample data
expenditure = [105, 120, 130, 125, 140, 110, 135, 145, 125, 115, 140, 150, 
               120, 155, 135, 130, 125, 155, 145, 135, 110, 145, 160, 165, 
               130, 125, 150, 155, 165, 160, 135, 140, 120, 130, 145, 150, 
               165, 155, 160, 135, 120, 110, 155, 160, 165, 130, 145, 140, 135, 125] # truncated for brevity


# Frequency and density data
intervals = ["105-115", "115-125", "125-135", "135-145", "145-155", "155-165"]
frequencies = [4, 3, 8, 10, 9, 6]
densities = [0.008, 0.006, 0.016, 0.020, 0.018, 0.012]

fig, ax1 = plt.subplots(figsize=(6, 4))

# Plotting frequency on the primary y-axis
ax1.bar(intervals, frequencies, color='skyblue', alpha=0.6, label='Frequency')
ax1.set_xlabel('Expenditure ($)')
ax1.set_ylabel('Frequency', color='blue')
ax1.tick_params(axis='y', labelcolor='blue')
ax1.set_title('Frequency and Density of Monthly Expenditure on Groceries')

# Creating the secondary y-axis for the density
ax2 = ax1.twinx()
ax2.plot(intervals, densities, color='green', marker='o', label='Density', linewidth=2)
ax2.set_ylabel('Density', color='green')
ax2.tick_params(axis='y', labelcolor='green')

# Showing the plot
plt.tight_layout()
plt.show()

6. Types of Continuous Frequency Distributions:

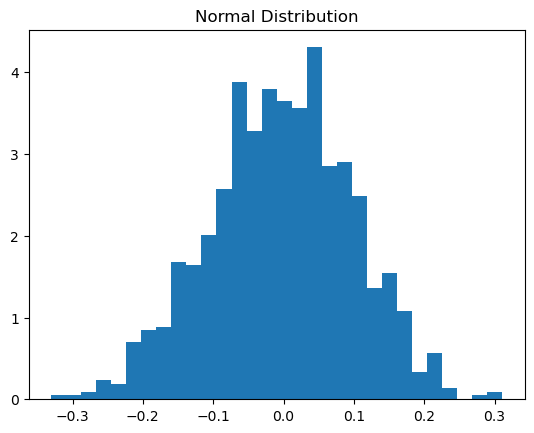
6.1. Normal (Gaussian) Distribution

Normal (Gaussian) Distribution: It’s bell-shaped and symmetric about the mean. Most of the observed values cluster around the mean, and the probabilities for values farther away from the mean taper off equally in both directions.

Application: Heights, IQ scores, and residuals in regression analysis usually follow this distribution.

import matplotlib.pyplot as plt
import numpy as np

mean, std_dev = 0, 0.1
s = np.random.normal(mean, std_dev, 1000)
plt.hist(s, 30, density=True)
plt.title('Normal Distribution')
plt.show()

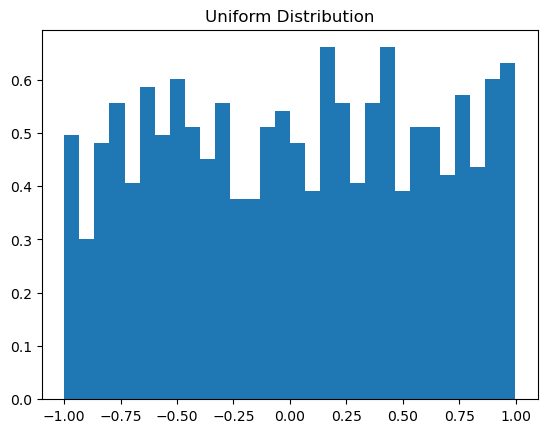
6.2. Uniform Distribution

Uniform Distribution: All values in a specified range are equally probable. It lacks a mode, and every interval of equal length on the distribution’s support is equally probable.

Example: The probability of any given number appearing when rolling a fair dice.

s = np.random.uniform(-1, 1, 1000)
plt.hist(s, 30, density=True)
plt.title('Uniform Distribution')
plt.show()

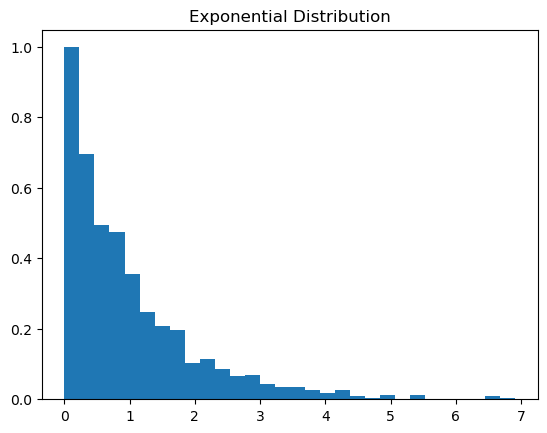
6.3. Exponential Distribution

Exponential Distribution: It describes the time intervals in a homogeneous Poisson process. Often used to model the time we need to wait before a given event occurs.

Application: Modeling the lifetime of an electronic component.

scale = 1.0
s = np.random.exponential(scale, 1000)
plt.hist(s, 30, density=True)
plt.title('Exponential Distribution')
plt.show()

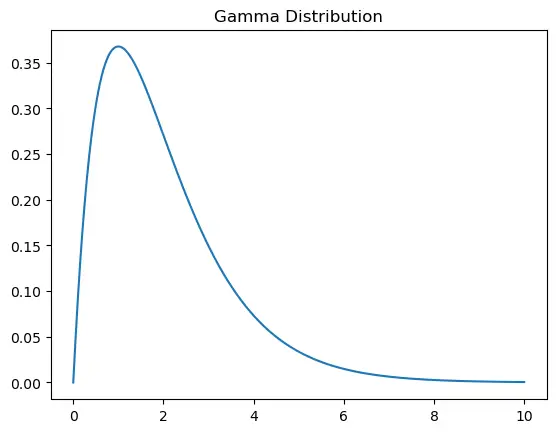
6.4. Gamma Distribution

Gamma Distribution: A two-parameter family of continuous probability distributions. It’s used for modeling the time until the nth event in a Poisson process.

Application: Modeling the sum of exponentially-distributed random variables.

import scipy.stats as stats

a = 2
s = np.linspace(0, 10, 1000)
y = stats.gamma.pdf(s, a)
plt.plot(s, y)
plt.title('Gamma Distribution')
plt.show()

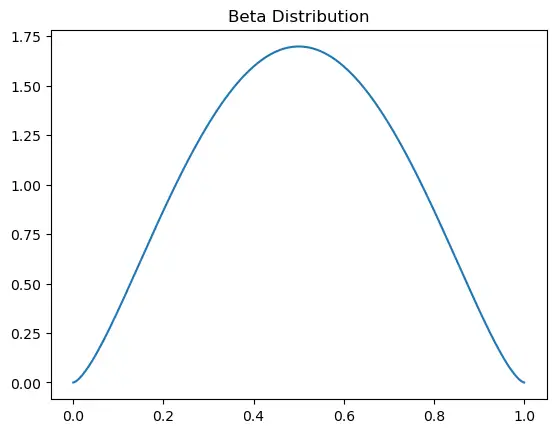
6.5. Beta Distribution

Beta Distribution: It’s defined on the interval [0,1] and is used to model random variables that have constraints on their range.

Application: Used in Bayesian analysis and to model random behavior in game theory.

a, b = 2.5, 2.5
s = np.linspace(0, 1, 1000)
y = stats.beta.pdf(s, a, b)
plt.plot(s, y)
plt.title('Beta Distribution')
plt.show()

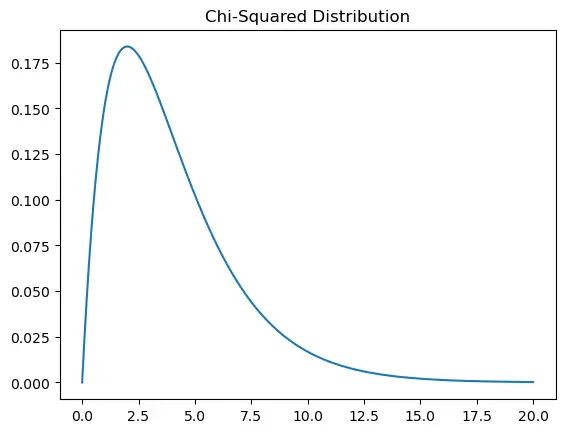
6.6. Chi-Squared Distribution

Chi-Squared Distribution: It’s related to the standard normal distribution. If you square a standard normal random variable, the resulting distribution is a chi-squared distribution with 1 degree of freedom.

Application: Used in hypothesis testing and confidence interval estimation for variance.

df = 4
s = np.linspace(0, 20, 1000)
y = stats.chi2.pdf(s, df)
plt.plot(s, y)
plt.title('Chi-Squared Distribution')
plt.show()

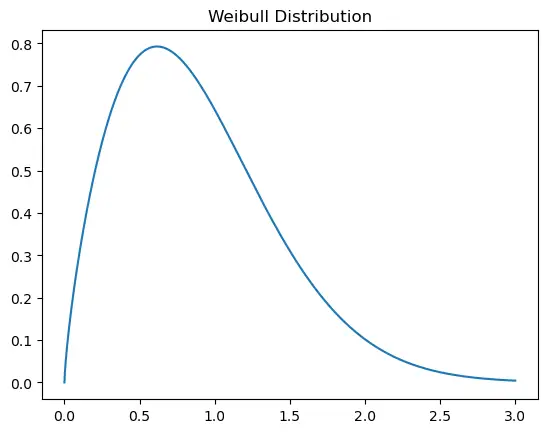
6.7. Weibull Distribution

Weibull Distribution: Used to analyze life data, model reliability data, and describe the time to failure of a process or system.

Application: Analyzing the time to first failure of a process.

c = 1.75
s = np.linspace(0, 3, 1000)
y = stats.weibull_min.pdf(s, c)
plt.plot(s, y)
plt.title('Weibull Distribution')
plt.show()

6.8. Log-Normal Distribution

Log-Normal Distribution: If the logarithm of a variable has a normal distribution, then the original variable has a log-normal distribution.

Application: Used to model stock prices and other financial data.

s = 0.954
x = np.linspace(0, 5, 1000)
pdf = stats.lognorm.pdf(x, s)
plt.plot(x, pdf)
plt.title('Log-Normal Distribution')
plt.show()

7. Conclusion:

Understanding and visualizing probability frequency distributions is essential for various applications from predicting future events, estimating risks, to making decisions under uncertainty.

Python, with its rich libraries like NumPy and Matplotlib, provides a simple yet powerful platform for anyone keen on diving into the world of probability and statistics. So, harness this knowledge, and make your data speak the language of probability.