Matplotlib is the most popular Python library to plot beautiful graphs. This tutorial guides you to grasp fundamental plotting through reproducible examples.

Useful Posts:
1. Matplotlib Beginners Tutorial
2. Top 50 Matplotlib Plots for Data Analysis
Overview
This tutorial takes you through the following well-rounded concepts:
1. Plotting your first graph
2. Line style and color
3. Saving a figure
4. Subplots
5. Multiple figures
6. Pyplot’s state machine: implicit vs explicit
7. Pylab vs Pyplot vs Matplotlib
8. Drawing text
9. Legends
10. Non-linear scales
11. Ticks and tickers
12. Polar projection
13. 3D projection
14. Scatter plot
15. Lines
16. Histograms
17. Images
18. Animations
19. Saving animations to video files
20. What next?
Plotting your first graph
First we need to import the matplotlib library.
import matplotlib
Matplotlib can output graphs using various backend graphics libraries, such as Tk, wxPython, etc. When running python using the command line, the graphs are typically shown in a separate window.
However, in a Jupyter notebook, we can simply output the graphs within the notebook itself by running the %matplotlib inline magic command.
%matplotlib inline
If you want to use Tk as your graphics backend, then run this instead.
matplotlib.use("TKAgg")
Now let’s plot our first graph! 🙂
import matplotlib.pyplot as plt
plt.plot([1, 2, 4, 9, 5, 3])
plt.show()
Yep, it’s as simple as calling the plot function with some data, and then calling the show function!
If the plot function is given one array of data, it will use it as the coordinates on the vertical axis, and it will just use each data point’s index in the array as the horizontal coordinate.
You can also provide two arrays: one for the horizontal axis x, and the second for the vertical axis y:
plt.plot([-3, -2, 5, 0], [1, 6, 4, 3])
plt.show()
The axes automatically match the extent of the data. We would like to give the graph a bit more room, so let’s call the axis function to change the extent of each axis [xmin, xmax, ymin, ymax].
plt.plot([-3, -2, 5, 0], [1, 6, 4, 3])
plt.axis([-4, 6, 0, 7])
plt.show()
Now, let’s plot a mathematical function. We use NumPy’s linspace function to create an array x containing 500 floats ranging from -2 to 2, then we create a second array y computed as the square of x (to learn about NumPy, read the NumPy tutorial).
import numpy as np
x = np.linspace(-2, 2, 500)
y = x**2
plt.plot(x, y)
plt.show()
That’s a bit dry, let’s add a title, and x and y labels, and draw a grid.
plt.plot(x, y)
plt.title("Square function")
plt.xlabel("x")
plt.ylabel("y = x**2")
plt.grid(True)
plt.show()
Line style and color
By default, matplotlib draws a line between consecutive points.
plt.plot([0, 100, 100, 0, 0, 100, 50, 0, 100], [0, 0, 100, 100, 0, 100, 130, 100, 0])
plt.axis([-10, 110, -10, 140])
plt.show()
You can pass a 3rd argument to change the line’s style and color.
For example "g--" means “green dashed line”.
plt.plot([0, 100, 100, 0, 0, 100, 50, 0, 100], [0, 0, 100, 100, 0, 100, 130, 100, 0], "g--")
plt.axis([-10, 110, -10, 140])
plt.show()
You can plot multiple lines on one graph very simply: just pass x1, y1, [style1], x2, y2, [style2], ...
For example:
plt.plot([0, 100, 100, 0, 0], [0, 0, 100, 100, 0], "r-", [0, 100, 50, 0, 100], [0, 100, 130, 100, 0], "g--")
plt.axis([-10, 110, -10, 140])
plt.show()
Or simply call plot multiple times before calling show.
plt.plot([0, 100, 100, 0, 0], [0, 0, 100, 100, 0], "r-")
plt.plot([0, 100, 50, 0, 100], [0, 100, 130, 100, 0], "g--")
plt.axis([-10, 110, -10, 140])
plt.show()
You can also draw simple points instead of lines. Here’s an example with green dashes, red dotted line and blue triangles.
Check out the documentation for the full list of style & color options.
x = np.linspace(-1.4, 1.4, 30)
plt.plot(x, x, 'g--', x, x**2, 'r:', x, x**3, 'b^')
plt.show()

The plot function returns a list of Line2D objects (one for each line). You can set extra attributes on these lines, such as the line width, the dash style or the alpha level. See the full list of attributes in the documentation.
x = np.linspace(-1.4, 1.4, 30)
line1, line2, line3 = plt.plot(x, x, 'g--', x, x**2, 'r:', x, x**3, 'b^')
line1.set_linewidth(3.0)
line1.set_dash_capstyle("round")
line3.set_alpha(0.2)
plt.show()
Saving a figure
Saving a figure to disk is as simple as calling savefig with the name of the file (or a file object). The available image formats depend on the graphics backend you use.
x = np.linspace(-1.4, 1.4, 30)
plt.plot(x, x**2)
plt.savefig("my_square_function.png", transparent=True)
Subplots
A matplotlib figure may contain multiple subplots. These subplots are organized in a grid. To create a subplot, just call the subplot function, and specify the number of rows and columns in the figure, and the index of the subplot you want to draw on (starting from 1, then left to right, and top to bottom).
Note that pyplot keeps track of the currently active subplot (which you can get a reference to by calling plt.gca()), so when you call the plot function, it draws on the active subplot.
x = np.linspace(-1.4, 1.4, 30)
plt.subplot(2, 2, 1) # 2 rows, 2 columns, 1st subplot = top left
plt.plot(x, x)
plt.subplot(2, 2, 2) # 2 rows, 2 columns, 2nd subplot = top right
plt.plot(x, x**2)
plt.subplot(2, 2, 3) # 2 rows, 2 columns, 3rd subplot = bottow left
plt.plot(x, x**3)
plt.subplot(2, 2, 4) # 2 rows, 2 columns, 4th subplot = bottom right
plt.plot(x, x**4)
plt.show()
- Note that
subplot(223)is a shorthand forsubplot(2, 2, 3).
It is easy to create subplots that span across multiple grid cells like so:
plt.subplot(2, 2, 1) # 2 rows, 2 columns, 1st subplot = top left
plt.plot(x, x)
plt.subplot(2, 2, 2) # 2 rows, 2 columns, 2nd subplot = top right
plt.plot(x, x**2)
plt.subplot(2, 1, 2) # 2 rows, *1* column, 2nd subplot = bottom
plt.plot(x, x**3)
plt.show()
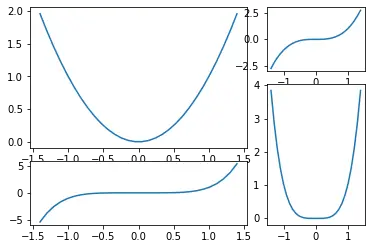
If you need more complex subplot positionning, you can use subplot2grid instead of subplot. You specify the number of rows and columns in the grid, then your subplot’s position in that grid (top-left = (0,0)), and optionally how many rows and/or columns it spans. For example:
plt.subplot2grid((3,3), (0, 0), rowspan=2, colspan=2)
plt.plot(x, x**2)
plt.subplot2grid((3,3), (0, 2))
plt.plot(x, x**3)
plt.subplot2grid((3,3), (1, 2), rowspan=2)
plt.plot(x, x**4)
plt.subplot2grid((3,3), (2, 0), colspan=2)
plt.plot(x, x**5)
plt.show()
If you need even more flexibility in subplot positioning, check out the GridSpec documentation
Multiple figures
It is also possible to draw multiple figures. Each figure may contain one or more subplots. By default, matplotlib creates figure(1) automatically. When you switch figure, pyplot keeps track of the currently active figure (which you can get a reference to by calling plt.gcf()), and the active subplot of that figure becomes the current subplot.
x = np.linspace(-1.4, 1.4, 30)
plt.figure(1)
plt.subplot(211)
plt.plot(x, x**2)
plt.title("Square and Cube")
plt.subplot(212)
plt.plot(x, x**3)
plt.figure(2, figsize=(10, 5))
plt.subplot(121)
plt.plot(x, x**4)
plt.title("y = x**4")
plt.subplot(122)
plt.plot(x, x**5)
plt.title("y = x**5")
plt.figure(1) # back to figure 1, current subplot is 212 (bottom)
plt.plot(x, -x**3, "r:")
plt.show()
Pyplot’s state machine: implicit vs explicit
So far we have used Pyplot’s state machine which keeps track of the currently active subplot. Every time you call the plot function, pyplot just draws on the currently active subplot. It also does some more magic, such as automatically creating a figure and a subplot when you call plot, if they don’t exist yet. This magic is convenient in an interactive environment (such as Jupyter).
But when you are writing a program, explicit is better than implicit. Explicit code is usually easier to debug and maintain, and if you don’t believe me just read the 2nd rule in the Zen of Python:
import this
#> The Zen of Python, by Tim Peters
#> Beautiful is better than ugly.
#> Explicit is better than implicit.
#> Simple is better than complex.
#> Complex is better than complicated.
#> Flat is better than nested.
#> Sparse is better than dense.
#> Readability counts.
#> Special cases aren't special enough to break the rules.
#> Although practicality beats purity.
#> Errors should never pass silently.
#> Unless explicitly silenced.
#> In the face of ambiguity, refuse the temptation to guess.
#> There should be one-- and preferably only one --obvious way to do it.
#> Although that way may not be obvious at first unless you're Dutch.
#> Now is better than never.
#> Although never is often better than *right* now.
#> If the implementation is hard to explain, it's a bad idea.
#> If the implementation is easy to explain, it may be a good idea.
#> Namespaces are one honking great idea -- let's do more of those!
Fortunately, Pyplot allows you to ignore the state machine entirely, so you can write beautifully explicit code. Simply call the subplots function and use the figure object and the list of axes objects that are returned. No more magic! For example:
x = np.linspace(-2, 2, 200)
fig1, (ax_top, ax_bottom) = plt.subplots(2, 1, sharex=True)
fig1.set_size_inches(10,5)
line1, line2 = ax_top.plot(x, np.sin(3*x**2), "r-", x, np.cos(5*x**2), "b-")
line3, = ax_bottom.plot(x, np.sin(3*x), "r-")
ax_top.grid(True)
fig2, ax = plt.subplots(1, 1)
ax.plot(x, x**2)
plt.show()
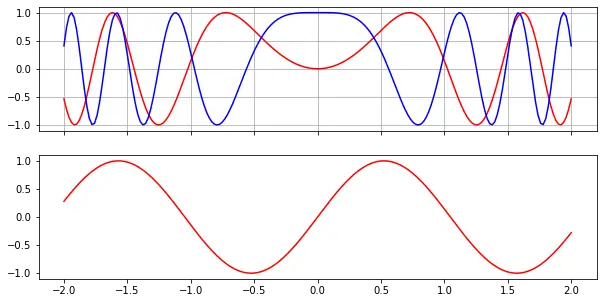
For consistency, we will continue to use pyplot’s state machine in the rest of this tutorial, but we recommend using the object-oriented interface in your programs.
Pylab vs Pyplot vs Matplotlib
There is some confusion around the relationship between pylab, pyplot and matplotlib. It’s simple: matplotlib is the full library, it contains everything including pylab and pyplot.
Pyplot provides a number of tools to plot graphs, including the state-machine interface to the underlying object-oriented plotting library.
Pylab is a convenience module that imports matplotlib.pyplot and NumPy in a single name space. You will find many examples using pylab, but it is no longer recommended (because explicit imports are better than implicit ones).
Drawing text
You can call text to add text at any location in the graph. Just specify the horizontal and vertical coordinates and the text, and optionally some extra attributes. Any text in matplotlib may contain TeX equation expressions, see the documentation for more details.
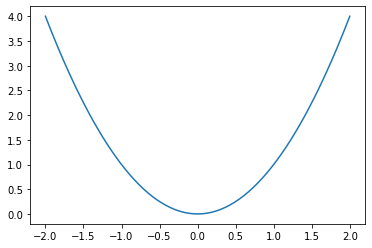
x = np.linspace(-1.5, 1.5, 30)
px = 0.8
py = px**2
plt.plot(x, x**2, "b-", px, py, "ro")
plt.text(0, 1.5, "Square function\n$y = x^2$", fontsize=20, color='blue', horizontalalignment="center")
plt.text(px - 0.08, py, "Beautiful point", ha="right", weight="heavy")
plt.text(px, py, "x = %0.2f\ny = %0.2f"%(px, py), rotation=50, color='gray')
plt.show()
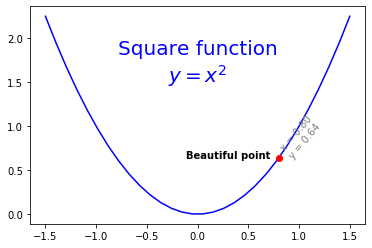
- Note:
hais an alias forhorizontalalignment
For more text properties, visit the documentation.
It is quite frequent to annotate elements of a graph, such as the beautiful point above. The annotate function makes this easy: just indicate the location of the point of interest, and the position of the text, plus optionally some extra attributes for the text and the arrow.
plt.plot(x, x**2, px, py, "ro")
plt.annotate("Beautiful point", xy=(px, py), xytext=(px-1.3,py+0.5),
color="green", weight="heavy", fontsize=14,
arrowprops={"facecolor": "lightgreen"})
plt.show()
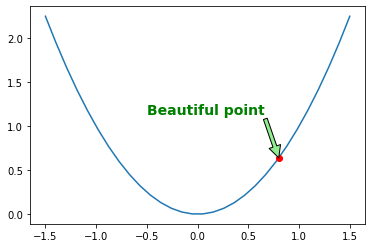
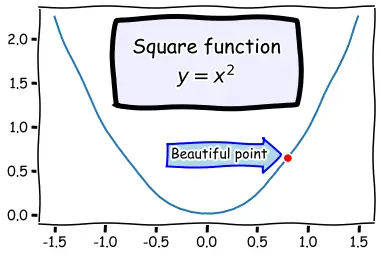
You can also add a bounding box around your text by using the bbox attribute:
plt.plot(x, x**2, px, py, "ro")
bbox_props = dict(boxstyle="rarrow,pad=0.3", ec="b", lw=2, fc="lightblue")
plt.text(px-0.2, py, "Beautiful point", bbox=bbox_props, ha="right")
bbox_props = dict(boxstyle="round4,pad=1,rounding_size=0.2", ec="black", fc="#EEEEFF", lw=5)
plt.text(0, 1.5, "Square function\n$y = x^2$", fontsize=20, color='black', ha="center", bbox=bbox_props)
plt.show()

Just for fun, if you want an xkcd-style plot, just draw within a with plt.xkcd() section:
with plt.xkcd():
plt.plot(x, x**2, px, py, "ro")
bbox_props = dict(boxstyle="rarrow,pad=0.3", ec="b", lw=2, fc="lightblue")
plt.text(px-0.2, py, "Beautiful point", bbox=bbox_props, ha="right")
bbox_props = dict(boxstyle="round4,pad=1,rounding_size=0.2", ec="black", fc="#EEEEFF", lw=5)
plt.text(0, 1.5, "Square function\n$y = x^2$", fontsize=20, color='black', ha="center", bbox=bbox_props)
plt.show()
Legends
The simplest way to add a legend is to set a label on all lines, then just call the legend function.
x = np.linspace(-1.4, 1.4, 50)
plt.plot(x, x**2, "r--", label="Square function")
plt.plot(x, x**3, "g-", label="Cube function")
plt.legend(loc="best")
plt.grid(True)
plt.show()

Non linear scales
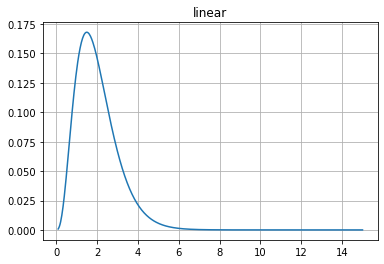
Matplotlib supports non-linear scales, such as logarithmic or logit scales.
x = np.linspace(0.1, 15, 500)
y = x**3/np.exp(2*x)
plt.figure(1)
plt.plot(x, y)
plt.yscale('linear')
plt.title('linear')
plt.grid(True)
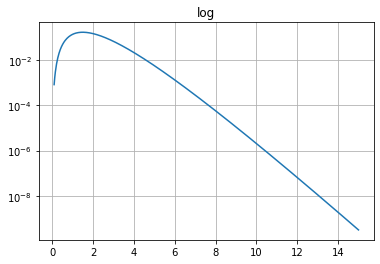
plt.figure(2)
plt.plot(x, y)
plt.yscale('log')
plt.title('log')
plt.grid(True)
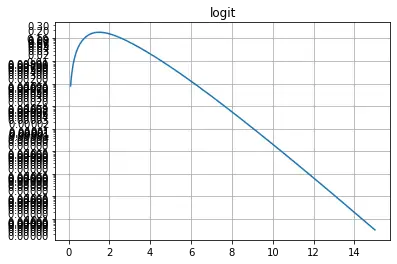
plt.figure(3)
plt.plot(x, y)
plt.yscale('logit')
plt.title('logit')
plt.grid(True)
plt.figure(4)
plt.plot(x, y - y.mean())
plt.yscale('symlog', linthreshy=0.05)
plt.title('symlog')
plt.grid(True)
plt.show()
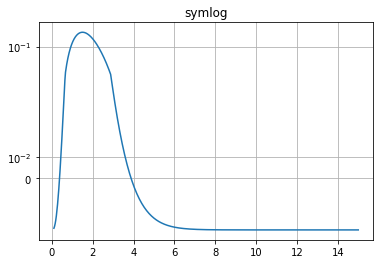
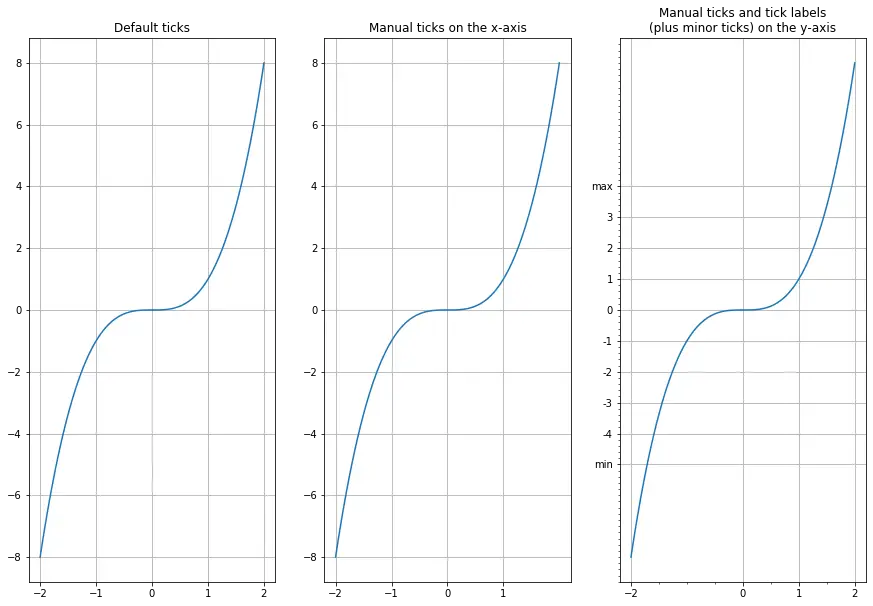
Ticks and tickers
The axes have little marks called “ticks”. To be precise, “ticks” are the locations of the marks (eg. (-1, 0, 1)), “tick lines” are the small lines drawn at those locations, “tick labels” are the labels drawn next to the tick lines, and “tickers” are objects that are capable of deciding where to place ticks. The default tickers typically do a pretty good job at placing ~5 to 8 ticks at a reasonable distance from one another.
But sometimes you need more control (eg. there are too many tick labels on the logit graph above). Fortunately, matplotlib gives you full control over ticks. You can even activate minor ticks.
x = np.linspace(-2, 2, 100)
plt.figure(1, figsize=(15,10))
plt.subplot(131)
plt.plot(x, x**3)
plt.grid(True)
plt.title("Default ticks")
ax = plt.subplot(132)
plt.plot(x, x**3)
ax.xaxis.set_ticks(np.arange(-2, 2, 1))
plt.grid(True)
plt.title("Manual ticks on the x-axis")
ax = plt.subplot(133)
plt.plot(x, x**3)
plt.minorticks_on()
ax.tick_params(axis='x', which='minor', bottom='off')
ax.xaxis.set_ticks([-2, 0, 1, 2])
ax.yaxis.set_ticks(np.arange(-5, 5, 1))
ax.yaxis.set_ticklabels(["min", -4, -3, -2, -1, 0, 1, 2, 3, "max"])
plt.title("Manual ticks and tick labels\n(plus minor ticks) on the y-axis")
plt.grid(True)
plt.show()
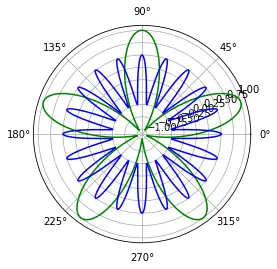
Polar projection
Drawing a polar graph is as easy as setting the projection attribute to "polar" when creating the subplot.
radius = 1
theta = np.linspace(0, 2*np.pi*radius, 1000)
plt.subplot(111, projection='polar')
plt.plot(theta, np.sin(5*theta), "g-")
plt.plot(theta, 0.5*np.cos(20*theta), "b-")
plt.show()
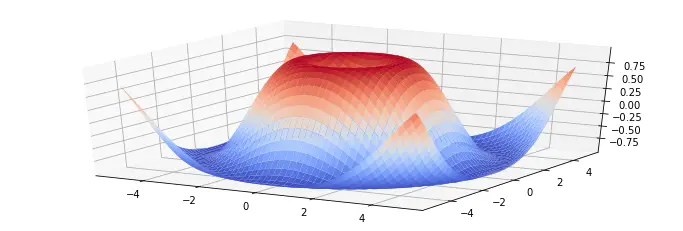
3D projection
Plotting 3D graphs is quite straightforward. You need to import Axes3D, which registers the "3d" projection. Then create a subplot setting the projection to "3d". This returns an Axes3DSubplot object, which you can use to call plot_surface, giving x, y, and z coordinates, plus optional attributes.
from mpl_toolkits.mplot3d import Axes3D
x = np.linspace(-5, 5, 50)
y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(x, y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
figure = plt.figure(1, figsize = (12, 4))
subplot3d = plt.subplot(111, projection='3d')
surface = subplot3d.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=matplotlib.cm.coolwarm, linewidth=0.1)
plt.show()
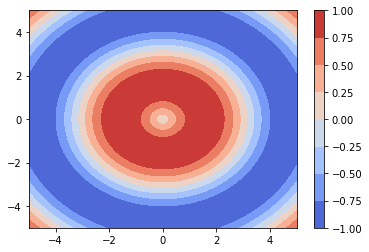
Another way to display this same data is via a contour plot.
plt.contourf(X, Y, Z, cmap=matplotlib.cm.coolwarm)
plt.colorbar()
plt.show()
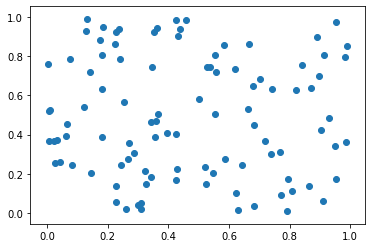
Scatter plot
To draw a scatter plot, simply provide the x and y coordinates of the points.
from numpy.random import rand
x, y = rand(2, 100)
plt.scatter(x, y)
plt.show()
You may also optionally provide the scale of each point.
x, y, scale = rand(3, 100)
scale = 500 * scale ** 5
plt.scatter(x, y, s=scale)
plt.show()

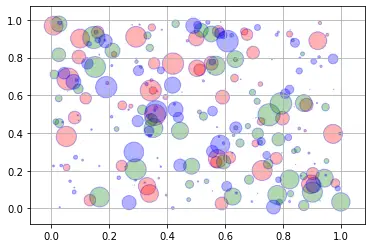
And as usual there are a number of other attributes you can set, such as the fill and edge colors and the alpha level.
for color in ['red', 'green', 'blue']:
n = 100
x, y = rand(2, n)
scale = 500.0 * rand(n) ** 5
plt.scatter(x, y, s=scale, c=color, alpha=0.3, edgecolors='blue')
plt.grid(True)
plt.show()
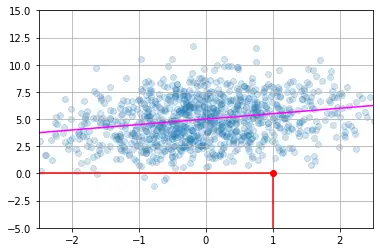
Lines
You can draw lines simply using the plot function, as we have done so far. However, it is often convenient to create a utility function that plots a (seemingly) infinite line across the graph, given a slope and an intercept. You can also use the hlines and vlines functions that plot horizontal and vertical line segments.
For example:
from numpy.random import randn
def plot_line(axis, slope, intercept, **kargs):
xmin, xmax = axis.get_xlim()
plt.plot([xmin, xmax], [xmin*slope+intercept, xmax*slope+intercept], **kargs)
x = randn(1000)
y = 0.5*x + 5 + randn(1000)*2
plt.axis([-2.5, 2.5, -5, 15])
plt.scatter(x, y, alpha=0.2)
plt.plot(1, 0, "ro")
plt.vlines(1, -5, 0, color="red")
plt.hlines(0, -2.5, 1, color="red")
plot_line(axis=plt.gca(), slope=0.5, intercept=5, color="magenta")
plt.grid(True)
plt.show()
Histograms
data = [1, 1.1, 1.8, 2, 2.1, 3.2, 3, 3, 3, 3]
plt.subplot(211)
plt.hist(data, bins = 10, rwidth=0.8)
plt.subplot(212)
plt.hist(data, bins = [1, 1.5, 2, 2.5, 3], rwidth=0.95)
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()

data1 = np.random.randn(400)
data2 = np.random.randn(500) + 3
data3 = np.random.randn(450) + 6
data4a = np.random.randn(200) + 9
data4b = np.random.randn(100) + 10
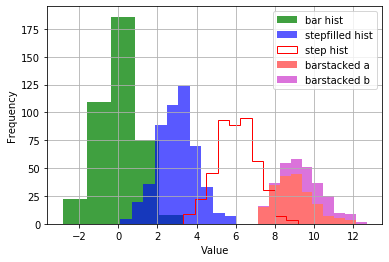
plt.hist(data1, bins=5, color='g', alpha=0.75, label='bar hist') # default histtype='bar'
plt.hist(data2, color='b', alpha=0.65, histtype='stepfilled', label='stepfilled hist')
plt.hist(data3, color='r', histtype='step', label='step hist')
plt.hist((data4a, data4b), color=('r','m'), alpha=0.55, histtype='barstacked', label=('barstacked a', 'barstacked b'))
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.legend()
plt.grid(True)
plt.show()
Images
Reading, generating and plotting images in matplotlib is quite straightforward.
To read an image, just import the matplotlib.image module, and call its imread function, passing it the file name (or file object). This returns the image data, as a NumPy array. Let’s try this with the my_square_function.png image we saved earlier.
import matplotlib.image as mpimg
img = mpimg.imread('my_square_function.png')
print(img.shape, img.dtype)
(288, 432, 4) float32
We have loaded a 288×432 image. Each pixel is represented by a 4-element array: red, green, blue, and alpha levels, stored as 32-bit floats between 0 and 1. Now all we need to do is to call imshow:
plt.imshow(img)
plt.show()

Tadaaa! You may want to hide the axes when you are displaying an image:
plt.imshow(img)
plt.axis('off')
plt.show()
It’s just as easy to generate your own image:
img = np.arange(100*100).reshape(100, 100)
print(img)
plt.imshow(img)
plt.show()
#> [[ 0 1 2 ... 97 98 99]
#> [ 100 101 102 ... 197 198 199]
#> [ 200 201 202 ... 297 298 299]
#> ...
#> [9700 9701 9702 ... 9797 9798 9799]
#> [9800 9801 9802 ... 9897 9898 9899]
#> [9900 9901 9902 ... 9997 9998 9999]]
As we did not provide RGB levels, the imshow function automatically maps values to a color gradient. By default, the color gradient goes from blue (for low values) to red (for high values), but you can select another color map. For example:
plt.imshow(img, cmap="hot")
plt.show()
You can also generate an RGB image directly:
img = np.empty((20,30,3))
img[:, :10] = [0, 0, 0.6]
img[:, 10:20] = [1, 1, 1]
img[:, 20:] = [0.6, 0, 0]
plt.imshow(img)
plt.show()

Since the img array is just quite small (20×30), when the imshow function displays it, it grows the image to the figure’s size. Imagine stretching the original image, leaving blanks between the original pixels.
How does imshow fill the blanks?
Well, by default, it just colors each blank pixel using the color of the nearest non-blank pixel. This technique can lead to pixelated images. If you prefer, you can use a different interpolation method, such as bilinear interpolation to fill the blank pixels. This leads to blurry edges, which may be nicer in some cases:
plt.imshow(img, interpolation="bilinear")
plt.show()

Animations
Although matplotlib is mostly used to generate images, it is also capable of displaying animations. First, you need to import matplotlib.animation.
import matplotlib.animation as animation
In the following example, we start by creating data points, then we create an empty plot, we define the update function that will be called at every iteration of the animation, and finally, we add an animation to the plot by creating a FuncAnimation instance.
The FuncAnimation constructor takes a figure, an update function and optional arguments. We specify that we want a 50-frame long animation, with 100ms between each frame. At each iteration, FuncAnimation calls our update function and passes it the frame number num (from 0 to 49 in our case) followed by the extra arguments that we specified with fargs.
Our update function simply sets the line data to be the first num data points (so the data gets drawn gradually), and just for fun we also add a small random number to each data point so that the line appears to wiggle.
x = np.linspace(-1, 1, 100)
y = np.sin(x**2*25)
data = np.array([x, y])
fig = plt.figure()
line, = plt.plot([], [], "r-") # start with an empty plot
plt.axis([-1.1, 1.1, -1.1, 1.1])
plt.plot([-0.5, 0.5], [0, 0], "b-", [0, 0], [-0.5, 0.5], "b-", 0, 0, "ro")
plt.grid(True)
plt.title("Marvelous animation")
# this function will be called at every iteration
def update_line(num, data, line):
line.set_data(data[..., :num] + np.random.rand(2, num) / 25) # we only plot the first `num` data points.
return line,
line_ani = animation.FuncAnimation(fig, update_line, frames=50, fargs=(data, line), interval=100)
plt.close() # call close() to avoid displaying the static plot
Next, let’s display the animation. One option is to convert it to HTML5 code (using a <video> tag), and render this code using IPython.display.HTML:
from IPython.display import HTML
HTML(line_ani.to_html5_video())
Saving animations to video files
Matplotlib relies on 3rd-party libraries to write videos such as FFMPEG or ImageMagick. In this example, we will be using FFMPEG so be sure to install it first. To save the animation to the GIF format, you would need ImageMagick.
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
line_ani.save('my_wiggly_animation.mp4', writer=writer)
What next?
Now you know all the basics of matplotlib, but there are many more options available. The best way to learn more, is to visit the gallery or the top 50 plots, look at the images, choose a plot that you are interested in, then just copy the code in a Jupyter notebook and play around with it.
The corresponding notebook for this tutorial can be found here in github.





