Python’s Scikit Learn provides a convenient interface for topic modeling using algorithms like Latent Dirichlet allocation(LDA), LSI and Non-Negative Matrix Factorization.
In this tutorial, you will learn how to build the best possible LDA topic model and explore how to showcase the outputs as meaningful results.
Contents
1. Introduction
2. Load the packages
3. Import Newsgroups Text Data
4. Remove emails and newline characters
5. Tokenize and Clean-up using gensim’s simple_preprocess()
6. Lemmatization
7. Create the Document-Word matrix
8. Check the Sparsicity
9. Build LDA model with sklearn
10. Diagnose model performance with perplexity and log-likelihood
11. How to GridSearch the best LDA model?
12. How to see the best topic model and its parameters?
13. Compare LDA Model Performance Scores
14. How to see the dominant topic in each document?
15. Review topics distribution across documents
16. How to visualize the LDA model with pyLDAvis?
17. How to see the Topic’s keywords?
18. Get the top 15 keywords each topic
19. How to predict the topics for a new piece of text?
20. How to cluster documents that share similar topics and plot?
21. How to get similar documents for any given piece of text?
22. Conclusion
 How to build topic models with python sklearn. Photo by Sebastien Gabriel.
How to build topic models with python sklearn. Photo by Sebastien Gabriel.
1. Introduction
In the last tutorial you saw how to build topics models with LDA using gensim. In this tutorial, however, I am going to use python’s the most popular machine learning library – scikit learn.
With scikit learn, you have an entirely different interface and with grid search and vectorizers, you have a lot of options to explore in order to find the optimal model and to present the results.
In this tutorial, you will learn:
- How to clean and process text data?
- How to prepare the text documents to build topic models with scikit learn?
- How to build a basic topic model using LDA and understand the params?
- How to extract the topic’s keywords?
- How to gridsearch and tune for optimal model?
- How to get the dominant topics in each document?
- Review and visualize the topic keywords distribution
- How to predict the topics for a new piece of text?
- Cluster the documents based on topic distribution
- How to get most similar documents based on topics discussed?
A lot of exciting stuff ahead. Let’s roll!
2. Load the packages
The core package used in this tutorial is scikit-learn (sklearn).
Regular expressions re, gensim and spacy are used to process texts. pyLDAvis and matplotlib for visualization and numpy and pandas for manipulating and viewing data in tabular format.
Let’s import them.
# Run in terminal or command prompt
# python3 -m spacy download en
import numpy as np
import pandas as pd
import re, nltk, spacy, gensim
# Sklearn
from sklearn.decomposition import LatentDirichletAllocation, TruncatedSVD
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.model_selection import GridSearchCV
from pprint import pprint
# Plotting tools
import pyLDAvis
import pyLDAvis.sklearn
import matplotlib.pyplot as plt
%matplotlib inline
3. Import Newsgroups Text Data
I will be using the 20-Newsgroups dataset for this. This version of the dataset contains about 11k newsgroups posts from 20 different topics. This is available as newsgroups.json.
Since it is in a json format with a consistent structure, I am using pandas.read_json() and the resulting dataset has 3 columns as shown.
# Import Dataset
df = pd.read_json('https://raw.githubusercontent.com/selva86/datasets/master/newsgroups.json')
print(df.target_names.unique())
['rec.autos' 'comp.sys.mac.hardware' 'rec.motorcycles' 'misc.forsale'
'comp.os.ms-windows.misc' 'alt.atheism' 'comp.graphics'
'rec.sport.baseball' 'rec.sport.hockey' 'sci.electronics' 'sci.space'
'talk.politics.misc' 'sci.med' 'talk.politics.mideast'
'soc.religion.christian' 'comp.windows.x' 'comp.sys.ibm.pc.hardware'
'talk.politics.guns' 'talk.religion.misc' 'sci.crypt']
df.head(15)

4. Remove emails and newline characters
You can see many emails, newline characters and extra spaces in the text and it is quite distracting. Let’s get rid of them using regular expressions.
# Convert to list
data = df.content.values.tolist()
# Remove Emails
data = [re.sub('\S*@\S*\s?', '', sent) for sent in data]
# Remove new line characters
data = [re.sub('\s+', ' ', sent) for sent in data]
# Remove distracting single quotes
data = [re.sub("\'", "", sent) for sent in data]
pprint(data[:1])
['From: (wheres my thing) Subject: WHAT car is this!? Nntp-Posting-Host: '
'rac3.wam.umd.edu Organization: University of Maryland, College Park Lines: '
'15 I was wondering if anyone out there could enlighten me on this car I saw '
'the other day. It was a 2-door sports car, looked to be from the late 60s/ '
'early 70s. It was called a Bricklin. The doors were really small. In '
'addition, the front bumper was separate from the rest of the body. This is '
'all I know. If anyone can tellme a model name, engine specs, years of '
'production, where this car is made, history, or whatever info you have on '
'this funky looking car, please e-mail. Thanks, - IL ---- brought to you by '
'your neighborhood Lerxst ---- ']
5. Tokenize and Clean-up using gensim’s simple_preprocess()
The sentences look better now, but you want to tokenize each sentence into a list of words, removing punctuations and unnecessary characters altogether.
Gensim’s simple_preprocess() is great for this. Additionally I have set deacc=True to remove the punctuations.
def sent_to_words(sentences):
for sentence in sentences:
yield(gensim.utils.simple_preprocess(str(sentence), deacc=True)) # deacc=True removes punctuations
data_words = list(sent_to_words(data))
print(data_words[:1])
[['from', 'wheres', 'my', 'thing', 'subject', 'what', 'car', 'is', 'this', 'nntp', 'posting', 'host', 'rac', 'wam', 'umd', 'edu', 'organization', 'university', 'of', 'maryland', 'college', 'park', 'lines', 'was', 'wondering', 'if', 'anyone', 'out', 'there', 'could', 'enlighten', 'me', 'on', 'this', 'car', 'saw', 'the', 'other', 'day', (..truncated..)]]
6. Lemmatization
Lemmatization is a process where we convert words to its root word.
For example: ‘Studying’ becomes ‘Study’, ‘Meeting becomes ‘Meet’, ‘Better’ and ‘Best’ becomes ‘Good’.
The advantage of this is, we get to reduce the total number of unique words in the dictionary.
As a result, the number of columns in the document-word matrix (created by CountVectorizer in the next step) will be denser with lesser columns.
You can expect better topics to be generated in the end.
def lemmatization(texts, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV']):
"""https://spacy.io/api/annotation"""
texts_out = []
for sent in texts:
doc = nlp(" ".join(sent))
texts_out.append(" ".join([token.lemma_ if token.lemma_ not in ['-PRON-'] else '' for token in doc if token.pos_ in allowed_postags]))
return texts_out
# Initialize spacy 'en' model, keeping only tagger component (for efficiency)
# Run in terminal: python3 -m spacy download en
nlp = spacy.load('en', disable=['parser', 'ner'])
# Do lemmatization keeping only Noun, Adj, Verb, Adverb
data_lemmatized = lemmatization(data_words, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
print(data_lemmatized[:2])
['where s thing subject what car be nntp post host rac wam umd edu organization university maryland college park line be wonder anyone out there could enlighten car see other days be door sport car look be late early be call bricklin door be really small addition front bumper be separate rest body be know anyone can tellme model name engine spec year production where car be make history whatev info have funky look car mail thank bring neighborhood lerxst' (..truncated..
7. Create the Document-Word matrix
The LDA topic model algorithm requires a document word matrix as the main input.
You can create one using CountVectorizer. In the below code, I have configured the CountVectorizer to consider words that has occurred at least 10 times (min_df), remove built-in english stopwords, convert all words to lowercase, and a word can contain numbers and alphabets of at least length 3 in order to be qualified as a word.
So, to create the doc-word matrix, you need to first initialise the CountVectorizer class with the required configuration and then apply fit_transform to actually create the matrix.
Since most cells contain zeros, the result will be in the form of a sparse matrix to save memory.
If you want to materialize it in a 2D array format, call the todense() method of the sparse matrix like its done in the next step.
vectorizer = CountVectorizer(analyzer='word',
min_df=10, # minimum reqd occurences of a word
stop_words='english', # remove stop words
lowercase=True, # convert all words to lowercase
token_pattern='[a-zA-Z0-9]{3,}', # num chars > 3
# max_features=50000, # max number of uniq words
)
data_vectorized = vectorizer.fit_transform(data_lemmatized)
8. Check the Sparsicity
Sparsicity is nothing but the percentage of non-zero datapoints in the document-word matrix, that is data_vectorized.
Since most cells in this matrix will be zero, I am interested in knowing what percentage of cells contain non-zero values.
# Materialize the sparse data
data_dense = data_vectorized.todense()
# Compute Sparsicity = Percentage of Non-Zero cells
print("Sparsicity: ", ((data_dense > 0).sum()/data_dense.size)*100, "%")
Sparsicity: 0.775887569365 %
9. Build LDA model with sklearn
Everything is ready to build a Latent Dirichlet Allocation (LDA) model. Let’s initialise one and call fit_transform() to build the LDA model.
For this example, I have set the n_topics as 20 based on prior knowledge about the dataset. Later we will find the optimal number using grid search.
# Build LDA Model
lda_model = LatentDirichletAllocation(n_topics=20, # Number of topics
max_iter=10, # Max learning iterations
learning_method='online',
random_state=100, # Random state
batch_size=128, # n docs in each learning iter
evaluate_every = -1, # compute perplexity every n iters, default: Don't
n_jobs = -1, # Use all available CPUs
)
lda_output = lda_model.fit_transform(data_vectorized)
print(lda_model) # Model attributes
LatentDirichletAllocation(batch_size=128, doc_topic_prior=None,
evaluate_every=-1, learning_decay=0.7,
learning_method='online', learning_offset=10.0,
max_doc_update_iter=100, max_iter=10, mean_change_tol=0.001,
n_components=10, n_jobs=-1, n_topics=20, perp_tol=0.1,
random_state=100, topic_word_prior=None,
total_samples=1000000.0, verbose=0)
10. Diagnose model performance with perplexity and log-likelihood
A model with higher log-likelihood and lower perplexity (exp(-1. * log-likelihood per word)) is considered to be good. Let’s check for our model.
# Log Likelyhood: Higher the better
print("Log Likelihood: ", lda_model.score(data_vectorized))
# Perplexity: Lower the better. Perplexity = exp(-1. * log-likelihood per word)
print("Perplexity: ", lda_model.perplexity(data_vectorized))
# See model parameters
pprint(lda_model.get_params())
Log Likelihood: -9965645.21463
Perplexity: 2061.88393838
{'batch_size': 128,
'doc_topic_prior': None,
'evaluate_every': -1,
'learning_decay': 0.7,
'learning_method': 'online',
'learning_offset': 10.0,
'max_doc_update_iter': 100,
'max_iter': 10,
'mean_change_tol': 0.001,
'n_components': 10,
'n_jobs': -1,
'n_topics': 20,
'perp_tol': 0.1,
'random_state': 100,
'topic_word_prior': None,
'total_samples': 1000000.0,
'verbose': 0}
On a different note, perplexity might not be the best measure to evaluate topic models because it doesn’t consider the context and semantic associations between words.
This can be captured using topic coherence measure, an example of this is described in the gensim tutorial I mentioned earlier.
11. How to GridSearch the best LDA model?
The most important tuning parameter for LDA models is n_components (number of topics). In addition, I am going to search learning_decay (which controls the learning rate) as well.
Besides these, other possible search params could be learning_offset (downweigh early iterations. Should be > 1) and max_iter. These could be worth experimenting if you have enough computing resources.
Be warned, the grid search constructs multiple LDA models for all possible combinations of param values in the param_grid dict. So, this process can consume a lot of time and resources.
# Define Search Param
search_params = {'n_components': [10, 15, 20, 25, 30], 'learning_decay': [.5, .7, .9]}
# Init the Model
lda = LatentDirichletAllocation()
# Init Grid Search Class
model = GridSearchCV(lda, param_grid=search_params)
# Do the Grid Search
model.fit(data_vectorized)
GridSearchCV(cv=None, error_score='raise',
estimator=LatentDirichletAllocation(batch_size=128, doc_topic_prior=None,
evaluate_every=-1, learning_decay=0.7, learning_method=None,
learning_offset=10.0, max_doc_update_iter=100, max_iter=10,
mean_change_tol=0.001, n_components=10, n_jobs=1,
n_topics=None, perp_tol=0.1, random_state=None,
topic_word_prior=None, total_samples=1000000.0, verbose=0),
fit_params=None, iid=True, n_jobs=1,
param_grid={'n_topics': [10, 15, 20, 25, 30], 'learning_decay': [0.5, 0.7, 0.9]},
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=0)
12. How to see the best topic model and its parameters?
# Best Model
best_lda_model = model.best_estimator_
# Model Parameters
print("Best Model's Params: ", model.best_params_)
# Log Likelihood Score
print("Best Log Likelihood Score: ", model.best_score_)
# Perplexity
print("Model Perplexity: ", best_lda_model.perplexity(data_vectorized))
Best Model's Params: {'learning_decay': 0.9, 'n_topics': 10}
Best Log Likelyhood Score: -3417650.82946
Model Perplexity: 2028.79038336
13. Compare LDA Model Performance Scores
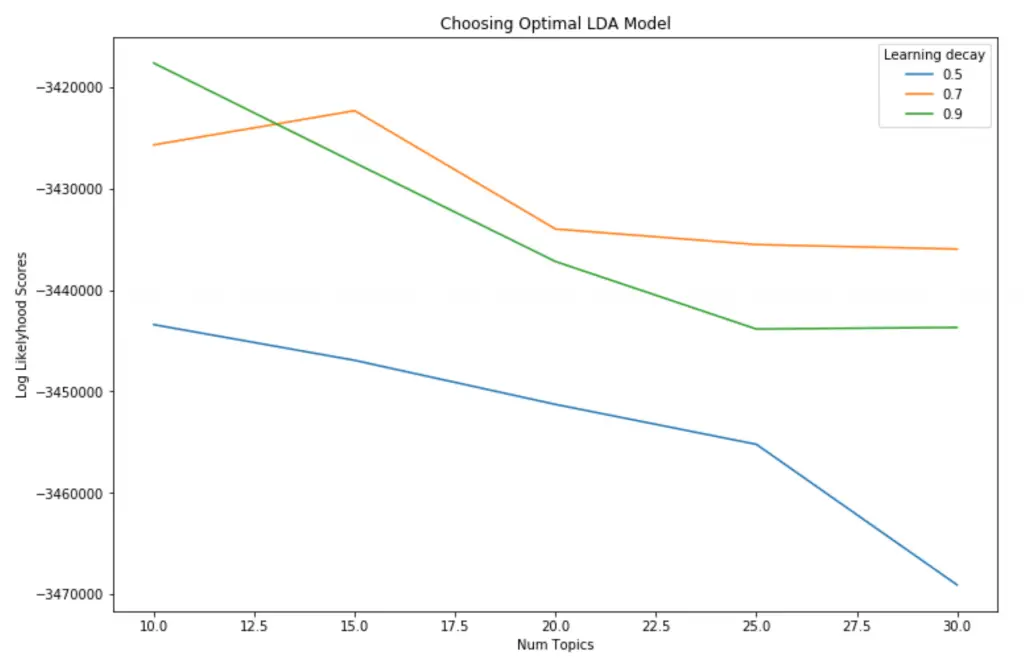
Plotting the log-likelihood scores against num_topics, clearly shows number of topics = 10 has better scores. And learning_decay of 0.7 outperforms both 0.5 and 0.9.
This makes me think, even though we know that the dataset has 20 distinct topics to start with, some topics could share common keywords.
For example, ‘alt.atheism’ and ‘soc.religion.christian’ can have a lot of common words. Same with ‘rec.motorcycles’ and ‘rec.autos’, ‘comp.sys.ibm.pc.hardware’ and ‘comp.sys.mac.hardware’, you get the idea.
To tune this even further, you can do a finer grid search for number of topics between 10 and 15. But I am going to skip that for now.
So the bottom line is, a lower optimal number of distinct topics (even 10 topics) may be reasonable for this dataset.
I don’t know that yet.
But LDA says so.
Let’s see.
# Get Log Likelyhoods from Grid Search Output
n_topics = [10, 15, 20, 25, 30]
log_likelyhoods_5 = [round(gscore.mean_validation_score) for gscore in model.grid_scores_ if gscore.parameters['learning_decay']==0.5]
log_likelyhoods_7 = [round(gscore.mean_validation_score) for gscore in model.grid_scores_ if gscore.parameters['learning_decay']==0.7]
log_likelyhoods_9 = [round(gscore.mean_validation_score) for gscore in model.grid_scores_ if gscore.parameters['learning_decay']==0.9]
# Show graph
plt.figure(figsize=(12, 8))
plt.plot(n_topics, log_likelyhoods_5, label='0.5')
plt.plot(n_topics, log_likelyhoods_7, label='0.7')
plt.plot(n_topics, log_likelyhoods_9, label='0.9')
plt.title("Choosing Optimal LDA Model")
plt.xlabel("Num Topics")
plt.ylabel("Log Likelyhood Scores")
plt.legend(title='Learning decay', loc='best')
plt.show()
14. How to see the dominant topic in each document?
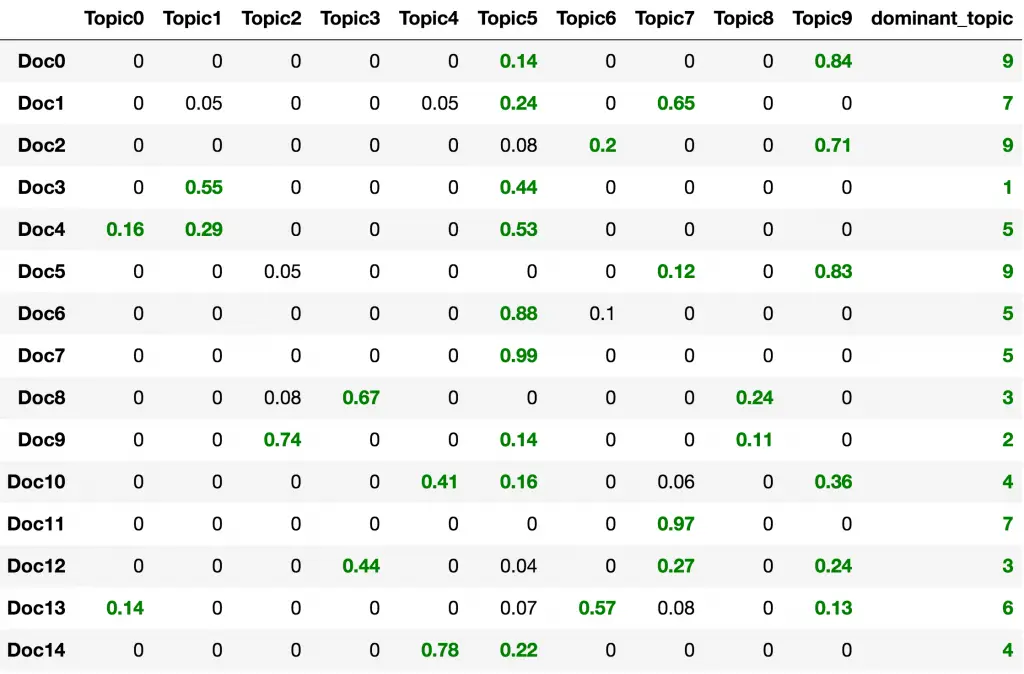
To classify a document as belonging to a particular topic, a logical approach is to see which topic has the highest contribution to that document and assign it.
In the table below, I’ve greened out all major topics in a document and assigned the most dominant topic in its own column.
# Create Document - Topic Matrix
lda_output = best_lda_model.transform(data_vectorized)
# column names
topicnames = ["Topic" + str(i) for i in range(best_lda_model.n_topics)]
# index names
docnames = ["Doc" + str(i) for i in range(len(data))]
# Make the pandas dataframe
df_document_topic = pd.DataFrame(np.round(lda_output, 2), columns=topicnames, index=docnames)
# Get dominant topic for each document
dominant_topic = np.argmax(df_document_topic.values, axis=1)
df_document_topic['dominant_topic'] = dominant_topic
# Styling
def color_green(val):
color = 'green' if val > .1 else 'black'
return 'color: {col}'.format(col=color)
def make_bold(val):
weight = 700 if val > .1 else 400
return 'font-weight: {weight}'.format(weight=weight)
# Apply Style
df_document_topics = df_document_topic.head(15).style.applymap(color_green).applymap(make_bold)
df_document_topics
15. Review topics distribution across documents
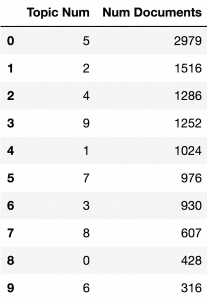
df_topic_distribution = df_document_topic['dominant_topic'].value_counts().reset_index(name="Num Documents")
df_topic_distribution.columns = ['Topic Num', 'Num Documents']
df_topic_distribution
16. How to visualize the LDA model with pyLDAvis?
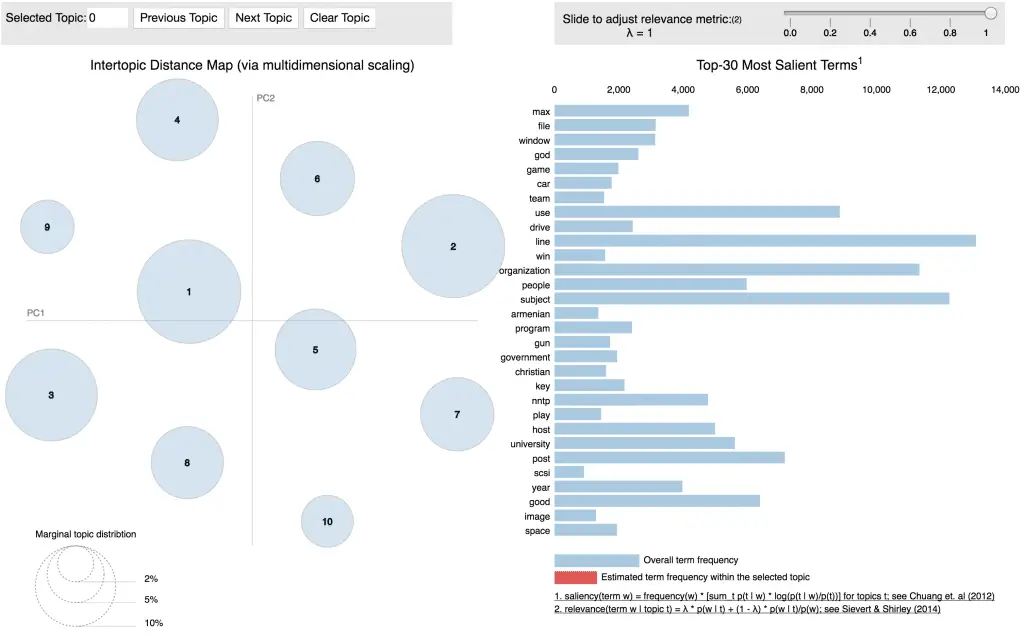
The pyLDAvis offers the best visualization to view the topics-keywords distribution.
A good topic model will have non-overlapping, fairly big sized blobs for each topic.
This seems to be the case here.
So, we are good.
pyLDAvis.enable_notebook()
panel = pyLDAvis.sklearn.prepare(best_lda_model, data_vectorized, vectorizer, mds='tsne')
panel
17. How to see the Topic’s keywords?
The weights of each keyword in each topic is contained in lda_model.components_ as a 2d array.
The names of the keywords itself can be obtained from vectorizer object using get_feature_names().
Let’s use this info to construct a weight matrix for all keywords in each topic.
# Topic-Keyword Matrix
df_topic_keywords = pd.DataFrame(best_lda_model.components_)
# Assign Column and Index
df_topic_keywords.columns = vectorizer.get_feature_names()
df_topic_keywords.index = topicnames
# View
df_topic_keywords.head()

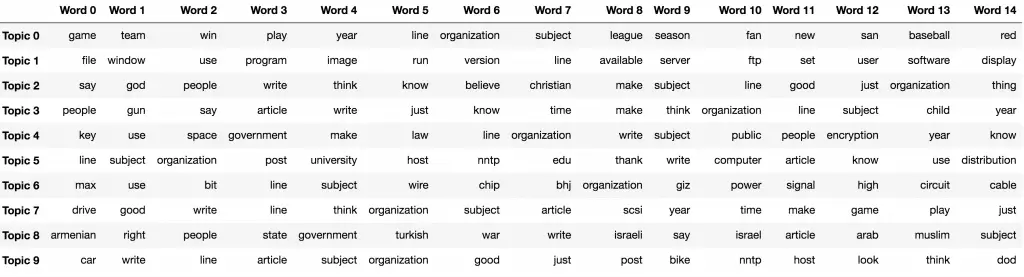
18. Get the top 15 keywords each topic
From the above output, I want to see the top 15 keywords that are representative of the topic.
The show_topics() defined below creates that.
# Show top n keywords for each topic
def show_topics(vectorizer=vectorizer, lda_model=lda_model, n_words=20):
keywords = np.array(vectorizer.get_feature_names())
topic_keywords = []
for topic_weights in lda_model.components_:
top_keyword_locs = (-topic_weights).argsort()[:n_words]
topic_keywords.append(keywords.take(top_keyword_locs))
return topic_keywords
topic_keywords = show_topics(vectorizer=vectorizer, lda_model=best_lda_model, n_words=15)
# Topic - Keywords Dataframe
df_topic_keywords = pd.DataFrame(topic_keywords)
df_topic_keywords.columns = ['Word '+str(i) for i in range(df_topic_keywords.shape[1])]
df_topic_keywords.index = ['Topic '+str(i) for i in range(df_topic_keywords.shape[0])]
df_topic_keywords
19. How to predict the topics for a new piece of text?
Assuming that you have already built the topic model, you need to take the text through the same routine of transformations and before predicting the topic.
For our case, the order of transformations is:
sent_to_words() –> lemmatization() –> vectorizer.transform() –> best_lda_model.transform()
You need to apply these transformations in the same order. So to simplify it, let’s combine these steps into a predict_topic() function.
# Define function to predict topic for a given text document.
nlp = spacy.load('en', disable=['parser', 'ner'])
def predict_topic(text, nlp=nlp):
global sent_to_words
global lemmatization
# Step 1: Clean with simple_preprocess
mytext_2 = list(sent_to_words(text))
# Step 2: Lemmatize
mytext_3 = lemmatization(mytext_2, allowed_postags=['NOUN', 'ADJ', 'VERB', 'ADV'])
# Step 3: Vectorize transform
mytext_4 = vectorizer.transform(mytext_3)
# Step 4: LDA Transform
topic_probability_scores = best_lda_model.transform(mytext_4)
topic = df_topic_keywords.iloc[np.argmax(topic_probability_scores), :].values.tolist()
return topic, topic_probability_scores
# Predict the topic
mytext = ["Some text about christianity and bible"]
topic, prob_scores = predict_topic(text = mytext)
print(topic)
['say', 'god', 'people', 'write', 'think', 'know', 'believe', 'christian', 'make', 'subject', 'line', 'good', 'just', 'organization', 'thing']
mytext has been allocated to the topic that has religion and Christianity related keywords, which is quite meaningful and makes sense.
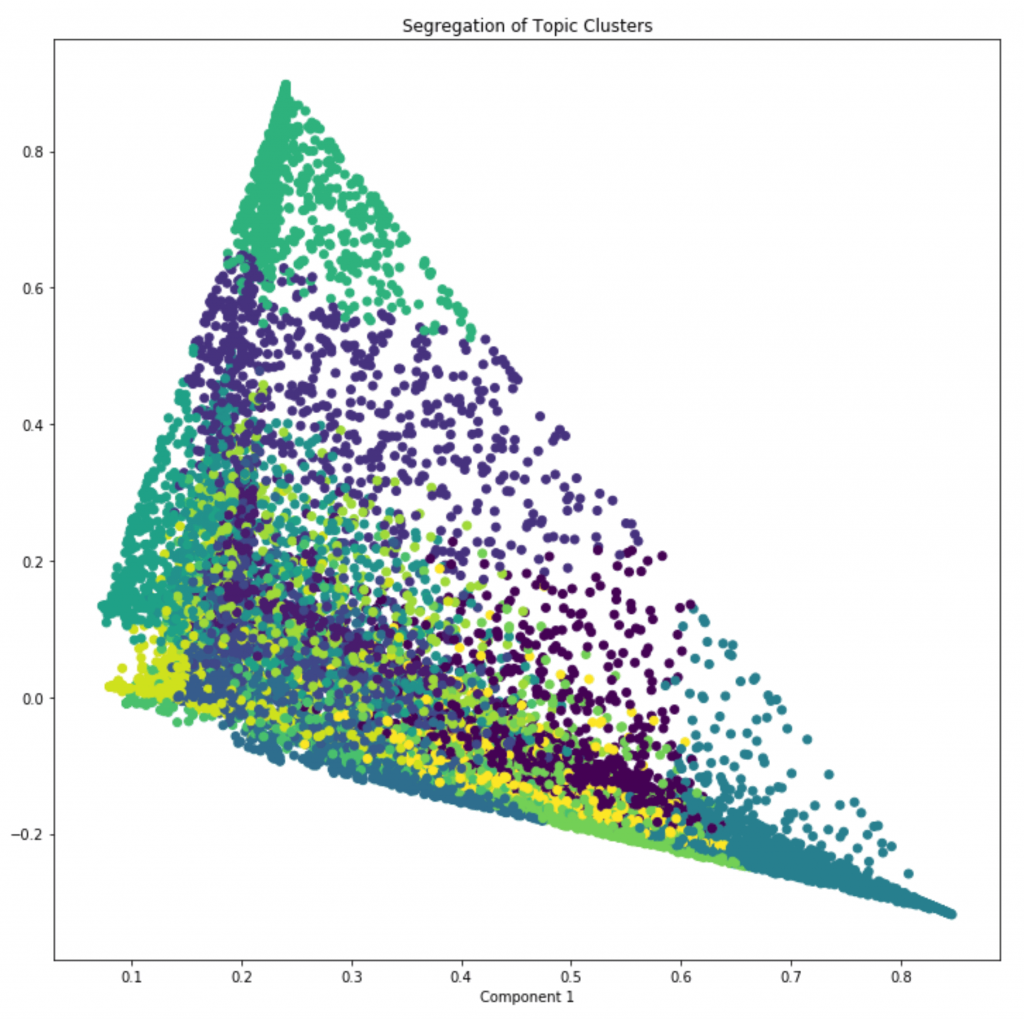
20. How to cluster documents that share similar topics and plot?
You can use k-means clustering on the document-topic probabilioty matrix, which is nothing but lda_output object. Since out best model has 15 clusters, I’ve set n_clusters=15 in KMeans().
Alternately, you could avoid k-means and instead, assign the cluster as the topic column number with the highest probability score.
We now have the cluster number. But we also need the X and Y columns to draw the plot.
For the X and Y, you can use SVD on the lda_output object with n_components as 2. SVD ensures that these two columns captures the maximum possible amount of information from lda_output in the first 2 components.
# Construct the k-means clusters
from sklearn.cluster import KMeans
clusters = KMeans(n_clusters=15, random_state=100).fit_predict(lda_output)
# Build the Singular Value Decomposition(SVD) model
svd_model = TruncatedSVD(n_components=2) # 2 components
lda_output_svd = svd_model.fit_transform(lda_output)
# X and Y axes of the plot using SVD decomposition
x = lda_output_svd[:, 0]
y = lda_output_svd[:, 1]
# Weights for the 15 columns of lda_output, for each component
print("Component's weights: \n", np.round(svd_model.components_, 2))
# Percentage of total information in 'lda_output' explained by the two components
print("Perc of Variance Explained: \n", np.round(svd_model.explained_variance_ratio_, 2))
Component's weights:
[[ 0.08 0.23 0.24 0.14 0.2 0.85 0.09 0.19 0.07 0.2 ]
[ 0.02 -0.1 0.9 0.16 0.16 -0.32 -0.01 -0.01 0.13 0.09]]
Perc of Variance Explained:
[ 0.09 0.21]
We have the X, Y and the cluster number for each document.
Let’s plot the document along the two SVD decomposed components. The color of points represents the cluster number (in this case) or topic number.
# Plot
plt.figure(figsize=(12, 12))
plt.scatter(x, y, c=clusters)
plt.xlabel('Component 2')
plt.xlabel('Component 1')
plt.title("Segregation of Topic Clusters", )
21. How to get similar documents for any given piece of text?
Once you know the probaility of topics for a given document (using predict_topic()), compute the euclidean distance with the probability scores of all other documents.
The most similar documents are the ones with the smallest distance.
from sklearn.metrics.pairwise import euclidean_distances
nlp = spacy.load('en', disable=['parser', 'ner'])
def similar_documents(text, doc_topic_probs, documents = data, nlp=nlp, top_n=5, verbose=False):
topic, x = predict_topic(text)
dists = euclidean_distances(x.reshape(1, -1), doc_topic_probs)[0]
doc_ids = np.argsort(dists)[:top_n]
if verbose:
print("Topic KeyWords: ", topic)
print("Topic Prob Scores of text: ", np.round(x, 1))
print("Most Similar Doc's Probs: ", np.round(doc_topic_probs[doc_ids], 1))
return doc_ids, np.take(documents, doc_ids)
# Get similar documents
mytext = ["Some text about christianity and bible"]
doc_ids, docs = similar_documents(text=mytext, doc_topic_probs=lda_output, documents = data, top_n=1, verbose=True)
print('\n', docs[0][:500])
Topic KeyWords: ['say', 'god', 'people', 'write', 'think', 'know', 'believe', 'christian', 'make', 'subject', 'line', 'good', 'just', 'organization', 'thing']
Topic Prob Scores of text: [[ 0. 0. 0.8 0. 0. 0. 0. 0. 0. 0. ]]
Most Similar Doc's Probs: [[ 0. 0. 0.8 0. 0. 0. 0.1 0. 0. 0. ]]
From: Subject: about Eliz C Prophet Lines: 21 Rob Butera asks about a book called THE LOST YEARS OF JESUS, by Elizabeth Clare Prophet. I do not know the book. However, Miss Prophet is the leader of a group (The Church Universal and Triumphant) derived from the I AM group founded by a Mr. Ballard who began his mission in the 1930s (I am writing this from memory and may not have all the details straight -- for an old account, check your library for a book by Marcus Bach) after an eighteenth-centu
22. Conclusion
We’ve covered some cutting-edge topic modeling approaches in this post.
If you managed to work this through, well done.
For those concerned about the time, memory consumption and variety of topics when building topic models check out the gensim tutorial on LDA.
I will meet you with a new tutorial next week.






