Gentle Introduction to Markov Chain

Markov Chains are a class of Probabilistic Graphical Models (PGM) that represent dynamic processes i.e., a process which is not static but rather changes with time. In particular, it concerns more about how the ‘state’ of a process changes with time.

All About Markov Chain. Photo by Juan Burgos.

Content

1. What is a Markov Chain
2. Three components of a Markov Chain
3. Properties of Markov Chain
4. How are the transition probabilities computed?
5. What problems can a Markov Chain model answer
6. How to estimate the parameters of a Markov chain
7. Convergence based on Perron-Frobenius Theorem

1. Introduction

Previously, we learned the basics of probability theory and graph theory and its use in the Probabilistic Graphical Models(PGM).

So, What is a Markov Chain?

Markov Chains are another class of PGMs that represents a dynamic process. That is, a process which is not static but rather changes with time. In particular, it concerns more about how the state of a process changes with time.

Let’s make it clear with an example.

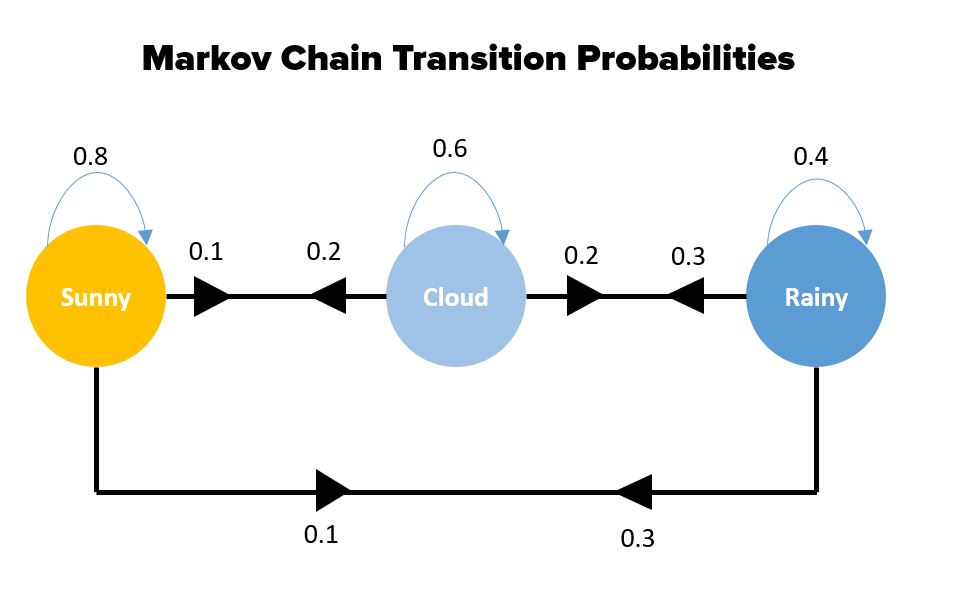
Let’s say, you want to model how the weather in a particular place changes over time. That means, you want to make a program for it. In a very simplified model (yes, it is always about the models in ML), we assume that the weather is constant throughout the day, and there can be only three possible states: Sunny, Cloudy, and Raining.

For any process to be considered for modeling with Markov Chain, it has to assume the Markov Property.

But what is a Markov Property?

Markov property states that, a state at time t+1 is dependent only on the current state ‘t’ and is independent of all previous states from t-1, t-2, . . .. In short, to know a future state, we just need to know the current state.

Thus, we can think of this simple weather model as a Markov chain in which there is state variable for any given day, with three possible values as stated above. These variables are linked in a chain, with a directed arc from one day to the next.

Three components of a Markov Chain

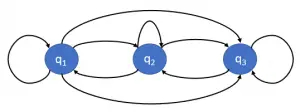
A Markov chain (MC) is a state machine that has a discrete number of states, q₁, q₂, . . . , q_n, and the transitions between states are nondeterministic, i.e., there is a probability of transiting from a state q_i to another state q_j : P(S_t = q_j | S_t−1 = q_i ).

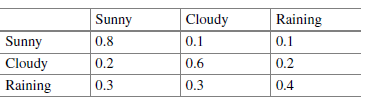
In our example, the three states are weather conditions: Sunny(q1), Cloudy(q2) and Rainy(q3)

Time is also discrete, such that the chain can be at a certain state q_i for each time step t. It satisfies the Markov property, that is, the probability of the next state depends only on the current state.

Formally, a Markov chain is specified with following three items:

1. Set of states: Q = {q₁, q₂, . . . , q_n}
2. Vector of prior probabilities (probabilities of occurrence of each state): Π = {π₁, π₂, . . . , π_n}, where π_i = P(S₀ = q_i )
3. Matrix of transition probabilities (A matrix of probabilities of change in the state from one to another): A = {a_{i j} }, i = [1..n], j = [1..n], where a_{i j} = P(S_t = q _j | S_t−1 = q_i )

where n is the number of states, and S₀ is the initial state. In a compact way, an MC is represented as λ = {A,Π}.

Properties of a Markov Chain

A Markov chain satisfies the following properties:

1. Probability axioms i.e., sum of all probabilities should be one:
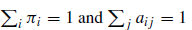
2. Markov property: P(S_t = q _j | S_t−1 = q_i , S_t−2 = q_k, . . .) = P(S_t = q _j | S_t−1 = q_i )

For example, consider the previous simple weather model with three states: q₁ = sunny, q₂ = cloudy, *q₃ = raining. In this case to specify an MC we will require a vector with three prior probabilities

And a 3 × 3 matrix of transition probabilities.

The transition matrix can be represented graphically with what is called a state transition diagram or simply a state diagram.

This diagram is a directed graph, where each node is a state and the arcs represent possible transitions between states.

If an arc between state q_i and q _j does not appear in the diagram, it means that the corresponding transition probability is zero. We saw an example of this diagram earlier in the post. Below is a more generic example of a state diagram.

How are the transition probabilities computed?

They are typically established over a long history of sequential data.

For example: Let’s say, we would know the sequence of sunny, cloudy and rainy days for a long duration, lets say 2 years. If in the 2 years, the total number of sunny days is 100, and out of that if the next day was a cloudy day 20 percent of the times, then the transition probability of Sunny -> Cloudy would be 20/100 = 0.2.

Likewise, all possible combinations are computed and the transition probability matrix is formed.

I will explain how to estimate all the parameters of a Markov chain shortly. But before that, let’s understand how the Markov Chain can practically be used.

What problems can a Markov Chain model answer

A Markov chain model can help answer the three basic problems/questions:

1. Problem 1: What is the probability of a certain state sequence?
2. Problem 2: What is the probability that the chain remains in a certain state for a period of time?
3. Problem 3: What is the expected time that the chain will remain in a certain state?

Let’s answer one-by-one, starting with Problem 1.

The probability of a sequence of states given the model is basically the product of the transition probabilities of the sequence of states:

where a_0i is the transition to the initial state in the sequence, which could be its prior probability (π_i ) or the transition from the previous state (if this is known).

For example, in the weather model, we might want to know the probability of the following sequence of states: Q = sunny, sunny, rainy, rainy, sunny, cloudy, sunny. Assuming that sunny is the initial state in the MC, then:

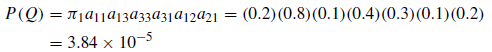
Now, let’s answer question 2.

The probability of staying d time steps in a certain state, q_i , is equivalent to the probability of a sequence in this state for d − 1 time steps and then transiting to a different state. That is,

Considering the weather model, what is the probability of three cloudy days? This can be computed as follows:

Hope that is clear?

Now lets do question 3: what is the expected time a Markov chain will remain in a certain state?

The average duration of a state sequence in a certain state is the expected value of the number of stages in that state, that is,. Substituting and we obatin,

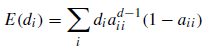
How to estimate the parameters of a Markov chain

Another important question is how to determine the parameters of the model, which is known as parameter estimation.

For an MC, the parameters can be estimated simply by counting the number of times that the sequence is in a certain state, i , and the number of times there is a transition from a state i to a state j.

Assume there are N sequences of observations. γ_0i is the number of times that the state i is the initial state in a sequence, γ_i is the number of times that we observe state i and γ_{i j} is the number of times that we observe a transition from state i to state j.

The parameters can be estimated with the following equations.

Initial probabilities:

Transition probabilities:

Note that for the last observed state in a sequence we do not observe the next state, so the last state for all the sequences is not considered in the counts.

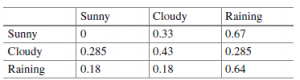
For instance, consider that for the weather example we have the following four observation sequences (q₁ = Sunny, q₂ = Cloudy, q₃ = Raining):

q2, q2, q3, q3, q3, q3, q1
q1, q3, q2, q3, q3, q3, q3
q3, q3, q2, q2
q2, q1, q2, q2, q1, q3, q1

Given these four sequences, the corresponding parameters can be estimated as
depicted as follows:

Calculated prior probabilities for the weather example,

Calculated transition probabilities for the weather example.

Convergence using Perron-Frobenius Theorem

An additional interesting question is: if a sequence transits from one state to another a large number of times, M, what is the probability (in the limit as M →∞) for each state q₀?

Given an initial probability vector, Π, and transition matrix, A, the probability of
each state, P = {p1, p2, . . . , pn} after M iterations is:

What happens when M → ∞? The solution is given by the Perron-Frobenius theorem, which says that when the following two conditions are satisfied:

1. Irreducibility: from every state i there is a probability a_{i j} > 0 of transiting to any state j .
2. Aperiodicity: the chain does not form cycles (a subset of states in which the chain
   remains once it transits to one of these state).

Then as M → ∞, the chain converges to an invariant distribution P, such that P × A = P, where A is the transition probability matrix.

The rate of convergence is determined by the second eigenvalue of matrix A.

For example, consider an MC with three states and the following transition probability matrix:

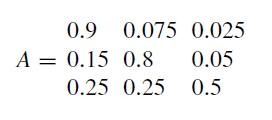
It can be shown that in this case the steady-state probabilities converge to P = {0.625, 0.3125, 0.0625}.

An interesting application of this convergence property of Markov chains for ranking web pages. We know should now discuss Hidden Markov Model (HMM).

This article was contributed by Pranay Lawhatre.