Affine Transformation – A Comprehensive Guide on Affine Transformation in Linear Algebra

The world of linear algebra is packed with fascinating concepts, and one of those is the affine transformation. If you’ve dabbled in computer graphics, image processing, or robotics, you’ve probably come across this term.

Let’s dive deep into affine transformations, breaking them down and illustrating their applications with examples.

What is an Affine Transformation?

An affine transformation is a specific type of transformation that maintains the collinearity between points (i.e., points lying on a straight line remain on a straight line) and preserves the ratios of distances between points lying on a straight line. Put simply, while shapes may change in size, rotation, or position through an affine transformation, their basic structure or parallelism is preserved.

Mathematically, an affine transformation can be expressed as:
$ T(\mathbf{v}) = A\mathbf{v} + \mathbf{b} $
Where:
– $ T(\mathbf{v}) $: Transformed vector.
– $ A $: Matrix representing the linear transformation.
– $ \mathbf{v} $: Original vector.
– $ \mathbf{b} $: Translation vector.

This equation shows that an affine transformation consists of two parts: a linear transformation (represented by matrix A) and a translation (represented by vector $ \mathbf{b} $).

Breaking Down Affine Transformations

1. Linear Transformation:
This involves operations like scaling, rotation, and shearing. A matrix multiplication represents the linear transformation of the vector.

2. Translation:
This is a shift of the vector in space. When you translate a vector, you’re essentially moving it without altering its orientation or length.

Example: A 2D Affine Transformation

Imagine you’re working with a 2D graphics program, and you’d like to transform a point in this space.

Linear Transformation:
Suppose you wish to stretch the graphic horizontally by a factor of 2 and vertically by a factor of 3. This action is expressed by the matrix:
$ A = \begin{bmatrix}
2 & 0 \\
0 & 3 \\
\end{bmatrix} $

Translation:
Next, you decide to shift the graphic one unit to the right and two units upward. This is represented by:
$ \mathbf{b} = \begin{bmatrix}
1 \\
2 \\
\end{bmatrix} $

Combining Both Operations:
Given a point $ \mathbf{p} = \begin{bmatrix}
1 \\
1 \\
\end{bmatrix} $, our affine transformation becomes:
$ T(\mathbf{p}) = A\mathbf{p} + \mathbf{b} $

Executing this, we find:
$ T(\mathbf{p}) = \begin{bmatrix}
3 \\
5 \\
\end{bmatrix} $
So, the point (1,1) is transformed to the point (3,5).

import numpy as np

def affine_transform(point, A, b):
    """Perform affine transformation on a point."""
    return np.dot(A, point) + b

# Define the transformation matrix A and translation vector b
A = np.array([[2, 0],
              [0, 3]])

b = np.array([1, 2])

# Define the point to be transformed
p = np.array([1, 1])

# Perform the affine transformation
transformed_point = affine_transform(p, A, b)

print(f"Original point: {p}")
print(f"Transformed point: {transformed_point}")

Original point: [1 1]
Transformed point: [3 5]

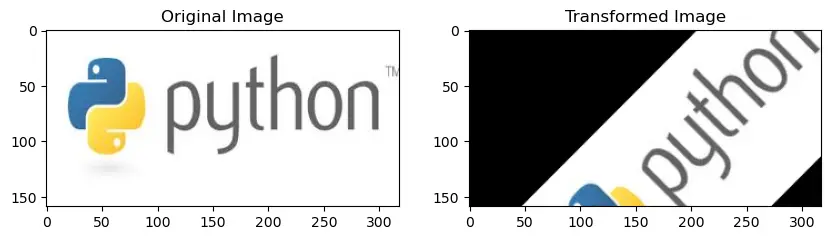
Use Case: Image Rotation and Translation Using Affine Transformation

Objective: We will rotate an image by a certain angle and then translate it by a specified amount using an affine transformation.

import numpy as np
import cv2
import matplotlib.pyplot as plt

def apply_affine_transform(img, angle, tx, ty):
    """
    Rotate the image by a specified angle and then translate it.

    Parameters:
    - img: The input image
    - angle: The rotation angle in degrees
    - tx, ty: The translation in x and y direction respectively
    """
    # Get the dimensions of the image
    rows, cols = img.shape[:2]

    # Calculate the center of the image
    center = (cols // 2, rows // 2)

    # Compute the rotation matrix
    rotation_matrix = cv2.getRotationMatrix2D(center, angle, 1)

    # Modify the rotation matrix to include translation
    rotation_matrix[0, 2] += tx
    rotation_matrix[1, 2] += ty

    # Apply the affine transformation
    transformed_img = cv2.warpAffine(img, rotation_matrix, (cols, rows))

    return transformed_img

# Load an image
img = cv2.imread('images.jpg')

# Ensure the image was loaded correctly
if img is None:
    print("Error: Image not loaded. Please check the image path.")
else:
    # Convert from BGR to RGB (OpenCV loads images in BGR)
    img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)

    # Apply the affine transformation
    angle = 45  # Rotate by 45 degrees
    tx, ty = 50, 30  # Translate by 50 units in x and 30 units in y
    result = apply_affine_transform(img_rgb, angle, tx, ty)

    # Display the original and transformed images using matplotlib
    plt.figure(figsize=(10, 5))

    plt.subplot(1, 2, 1)
    plt.imshow(img_rgb)
    plt.title('Original Image')

    plt.subplot(1, 2, 2)
    plt.imshow(result)
    plt.title('Transformed Image')

    plt.show()

Applications of Affine Transformations

Affine transformations are pivotal in numerous domains:

1. Computer Graphics: For tasks like image scaling, rotation, and translation.
2. Robotics: In path planning and movement transformations.
3. Medical Imaging: For image registration, where images from different times or different modalities are aligned.

Conclusion

Affine transformations, with their capability to combine linear transformations and translations, provide a powerful tool in linear algebra. Whether you’re designing the next hit video game or working on cutting-edge robotics, understanding and mastering affine transformations can be invaluable. As always, the key is to practice, experiment, and see these transformations in action. Happy transforming!