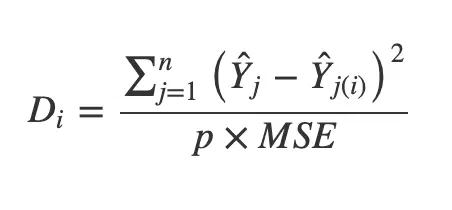Cook’s distance is a measure computed to measure the influence exerted by each observation on the trained model. It is measured by building a regression model and therefore is impacted only by the X variables included in the model.
What is Cooks Distance?
Cook’s distance measures the influence exerted by each data point (row / observation) on the predicted outcome.
The cook’s distance for each observation ‘i’ measures the change in Ŷ (fitted Y) for all observations with and without the presence of observation ‘i’, so we know how much the observation ‘i’ impacted the fitted values.
So you build a model with and without the observation ‘i’ in the dataset and see how much the predicted values of all other observations change.
Mathematically, cook’s distance Di for observation i is computed as:
where,
- Ŷ j is the value of jth fitted response when all the observations are included.
- Ŷ j(i) is the value of jth fitted response, where the fit does not include observation i.
- MSE is the mean squared error.
- p is the number of coefficients in the regression model.
Pros and Cons
Pros:
- Considers all variables in the model when calling out influential points.
- Formula based, intuitive to understand.
Cons:
- To compute Cook’s distance of each row, it requires the model to be retrained. So, computationally expensive to apply this method to other algorithms besides linear regression.
Let’s Compute Cook’s distance in Python.
It can be directly computed using the Statsmodels package. But first, let’s build the regression model.
Step 1: Prepare Data
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
filename = "https://archive.ics.uci.edu/ml/machine-learning-databases/autos/imports-85.data"
headers = ["symboling","normalized-losses","make","fuel-type","aspiration", "num-of-doors","body-style",
"drive-wheels","engine-location","wheel-base", "length","width","height","curb-weight","engine-type",
"num-of-cylinders", "engine-size","fuel-system","bore","stroke","compression-ratio","horsepower",
"peak-rpm","city-mpg","highway-mpg","price"]
df = pd.read_csv(filename, names = headers)
df.head()
| symboling | normalized-losses | make | fuel-type | aspiration | num-of-doors | body-style | drive-wheels | engine-location | wheel-base | … | engine-size | fuel-system | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | ? | alfa-romero | gas | std | two | convertible | rwd | front | 88.6 | … | 130 | mpfi | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 13495 |
| 1 | 3 | ? | alfa-romero | gas | std | two | convertible | rwd | front | 88.6 | … | 130 | mpfi | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 16500 |
| 2 | 1 | ? | alfa-romero | gas | std | two | hatchback | rwd | front | 94.5 | … | 152 | mpfi | 2.68 | 3.47 | 9.0 | 154 | 5000 | 19 | 26 | 16500 |
| 3 | 2 | 164 | audi | gas | std | four | sedan | fwd | front | 99.8 | … | 109 | mpfi | 3.19 | 3.40 | 10.0 | 102 | 5500 | 24 | 30 | 13950 |
| 4 | 2 | 164 | audi | gas | std | four | sedan | 4wd | front | 99.4 | … | 136 | mpfi | 3.19 | 3.40 | 8.0 | 115 | 5500 | 18 | 22 | 17450 |
5 rows × 26 columns
Data cleaning
df = df.loc[:, ['symboling', 'wheel-base', 'engine-size', 'bore', 'stroke',
'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg',
'highway-mpg', 'price']]
df = df.replace('?', np.nan)
df = df.dropna()
df.reset_index(drop = True, inplace = True)
df.head()
| symboling | wheel-base | engine-size | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 88.6 | 130 | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 13495 |
| 1 | 3 | 88.6 | 130 | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 16500 |
| 2 | 1 | 94.5 | 152 | 2.68 | 3.47 | 9.0 | 154 | 5000 | 19 | 26 | 16500 |
| 3 | 2 | 99.8 | 109 | 3.19 | 3.40 | 10.0 | 102 | 5500 | 24 | 30 | 13950 |
| 4 | 2 | 99.4 | 136 | 3.19 | 3.40 | 8.0 | 115 | 5500 | 18 | 22 | 17450 |
Step 2 : Train linear regression model
import statsmodels.api as sm
#define response variable
y = df['price']
#define explanatory variable
x = df[['symboling', 'wheel-base', 'engine-size', 'bore', 'stroke',
'compression-ratio', 'horsepower', 'peak-rpm', 'city-mpg',
'highway-mpg']]
Build the linear regression model.
#add constant to predictor variables
x = sm.add_constant(x)
#fit linear regression model
model = sm.OLS(y.astype(float), x.astype(float)).fit()
Step 3 : Calculate Cook’s distance
#suppress scientific notation
import numpy as np
np.set_printoptions(suppress=True)
#create instance of influence
influence = model.get_influence()
Get the influence (Cook’s distance) scores
#obtain Cook's distance for each observation
cooks = influence.cooks_distance
#display Cook's distances
print(cooks)
(array([0.00005047, 0.00794651, 0.00235295, 0.00115412, 0.00229406,
0.00001475, 0.00040342, 0.00195747, 0.03696988, 0.00405958,
0.00509101, 0.00570949, 0.00620111, 0.01803001, 0.00335913,
0.07252824, 0.02556543, 0.04585015, 0.00000023, 0.00011847,
0.00000804, 0.00001075, 0.00001616, 0.00002787, 0.00000096,
0.00017893, 0.00003149, 0.00153593, 0.00321647, 0.05605546,
0.00023964, 0.0002776 , 0.00017649, 0.00000042, 0.00005717,
0.00005307, 0.00111793, 0.00011928, 0.00024373, 0.00013439,
0.00343908, 0.00001979, 0.00038317, 0.00006676, 0.00001466,
0.01387144, 0.67290488, 0.00029421, 0.00003223, 0.00022211,
0.00018456, 0.00050611, 0.00026183, 0.00039154, 0.000035 ,
0.0000165 , 0.00224472, 0.00031293, 0.00134812, 0.01269743,
0.00220525, 0.01360418, 0.01752224, 0.03048843, 0.00608054,
0.0820174 , 0.00601548, 0.06747548, 0.00295536, 0.00032691,
0.00016934, 0.00003394, 0.00003416, 0.00056306, 0.00151128,
0.00449227, 0.00008387, 0.00036013, 0.0020883 , 0.00080219,
0.00052908, 0.00073918, 0.00012555, 0.0017916 , 0.00000065,
0.00000839, 0.00006592, 0.00005771, 0.00016434, 0.00009382,
0.00022227, 0.00031158, 0.00052463, 0.00020926, 0.02253932,
0.01824963, 0.02049076, 0.007906 , 0.00873687, 0.00393047,
0.00092289, 0.01260195, 0.0056554 , 0.02883812, 0.00116899,
0.00057631, 0.00373692, 0.00311193, 0.00334457, 0.00000108,
0.00000342, 0.00000767, 0.00001616, 0.00002787, 0.00000096,
0.00000048, 0.00152386, 0.00403854, 0.01077807, 0.03652447,
0.06101313, 0.1287357 , 0.00197229, 0.00068141, 0.04555418,
0.00074255, 0.00214108, 0.00346266, 0.00702787, 0.00057118,
0.00005023, 0.00305842, 0.00066841, 0.00057935, 0.00003855,
0.00019247, 0.00160212, 0.00039846, 0.00206929, 0.00586846,
0.00000056, 0.00001257, 0.00003468, 0.00032255, 0.00158363,
0.00318834, 0.00000002, 0.00001426, 0.00186318, 0.00721941,
0.00078872, 0.00046616, 0.00120741, 0.00042025, 0.00052502,
0.0057842 , 0.00466251, 0.00925114, 0.00592447, 0.00508653,
0.00268166, 0.00212835, 0.00277433, 0.00000584, 0.0008918 ,
0.00041052, 0.00181117, 0.00261463, 0.02421767, 0.02716114,
0.01624373, 0.01152021, 0.00650464, 0.00052591, 0.00533062,
0.00039766, 0.00025162, 0.00000374, 0.00016362, 0.00156563,
0.00007099, 0.00105815, 0.01155108, 0.00050471, 0.00767723,
0.00446398, 0.00002331, 0.00001264, 0.00493016, 0.00522982,
0.00044824, 0.00037132, 0.00378943, 0.0084261 , 0.01092127]), array([1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 0.99999948, 1. ,
1. , 1. , 1. , 0.99999999, 1. ,
0.99998228, 0.99999993, 0.99999838, 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 0.99999534,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 0.76302816, 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 0.99999999, 0.99999981, 1. ,
0.99996672, 1. , 0.99998779, 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 0.99999996,
0.99999999, 0.99999998, 1. , 1. , 1. ,
1. , 1. , 1. , 0.99999986, 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 0.99999951,
0.99999276, 0.99968315, 1. , 1. , 0.99999843,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 0.99999995, 0.9999999 ,
0.99999999, 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ,
1. , 1. , 1. , 1. , 1. ]))
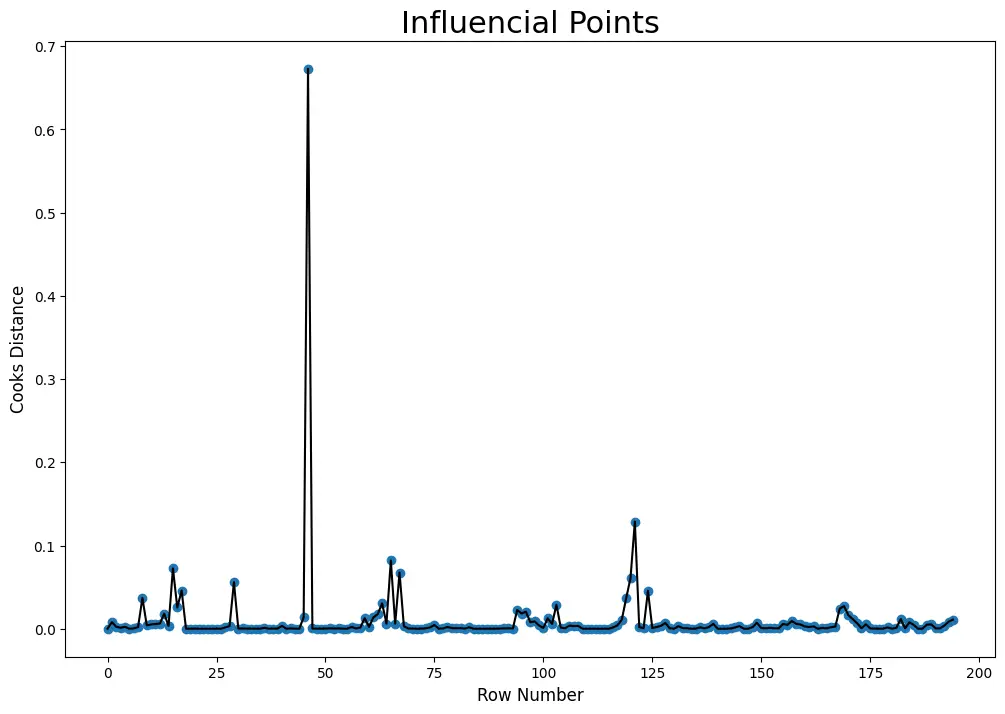
Step 4: Visualize the cook’s distance and find influencial points
The rows which have cook’s distance greater than 4x of mean cook’s distance are known as influencial points
# Draw plot
plt.figure(figsize = (12, 8))
plt.scatter(df.index, cooks[0])
plt.plot(df.index, cooks[0], color='black')
plt.xlabel('Row Number', fontsize = 12)
plt.ylabel('Cooks Distance', fontsize = 12)
plt.title('Influencial Points', fontsize = 22)
plt.show()
Mean Cook’s distance
mean_cooks = np.mean(cooks[0])
mean_cooks
0.00990911857380304
mean_cooks_list = [4*mean_cooks for i in df.index]
# mean_cooks_list
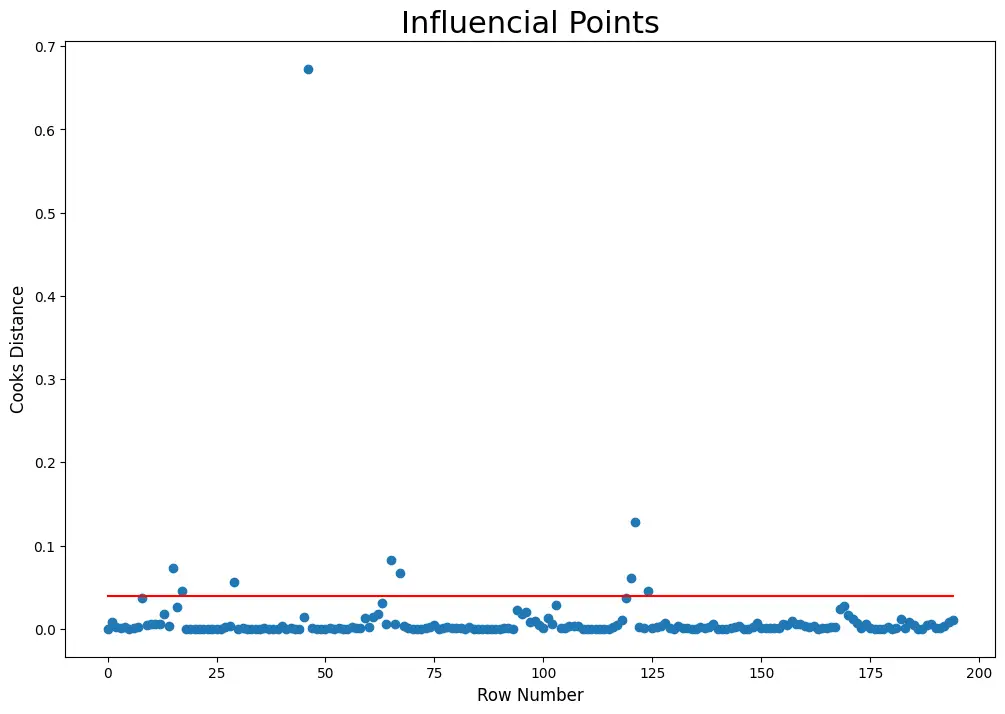
Visualize the Influence scores
# Draw plot
plt.figure(figsize = (12, 8))
plt.scatter(df.index, cooks[0])
plt.plot(df.index, mean_cooks_list, color="red")
plt.xlabel('Row Number', fontsize = 12)
plt.ylabel('Cooks Distance', fontsize = 12)
plt.title('Influencial Points', fontsize = 22)
plt.show()
# Influencial points
influencial_points = df.index[cooks[0] > 4*mean_cooks]
influencial_points
Int64Index([15, 17, 29, 46, 65, 67, 120, 121, 124], dtype=’int64′)
df.iloc[influencial_points, :]
| symboling | wheel-base | engine-size | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 15 | 0 | 103.5 | 209 | 3.62 | 3.39 | 8.0 | 182 | 5400 | 16 | 22 | 41315 |
| 17 | 2 | 88.4 | 61 | 2.91 | 3.03 | 9.5 | 48 | 5100 | 47 | 53 | 5151 |
| 29 | 2 | 86.6 | 92 | 2.91 | 3.41 | 9.6 | 58 | 4800 | 49 | 54 | 6479 |
| 46 | 0 | 102.0 | 326 | 3.54 | 2.76 | 11.5 | 262 | 5000 | 13 | 17 | 36000 |
| 65 | 3 | 96.6 | 234 | 3.46 | 3.10 | 8.3 | 155 | 4750 | 16 | 18 | 35056 |
| 67 | 1 | 112.0 | 304 | 3.80 | 3.35 | 8.0 | 184 | 4500 | 14 | 16 | 45400 |
| 120 | 3 | 89.5 | 194 | 3.74 | 2.90 | 9.5 | 207 | 5900 | 17 | 25 | 34028 |
| 121 | 3 | 89.5 | 194 | 3.74 | 2.90 | 9.5 | 207 | 5900 | 17 | 25 | 37028 |
| 124 | 3 | 99.1 | 121 | 2.54 | 2.07 | 9.3 | 110 | 5250 | 21 | 28 | 15040 |
Let’s look at non influential points as well
When you compare, some features of the influential data points are towards an extreme.
# Non Influencial points
noninfluencial_points = df.index[cooks[0] < 4*mean_cooks]
noninfluencial_points
df.iloc[noninfluencial_points, :].head()
| symboling | wheel-base | engine-size | bore | stroke | compression-ratio | horsepower | peak-rpm | city-mpg | highway-mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 88.6 | 130 | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 13495 |
| 1 | 3 | 88.6 | 130 | 3.47 | 2.68 | 9.0 | 111 | 5000 | 21 | 27 | 16500 |
| 2 | 1 | 94.5 | 152 | 2.68 | 3.47 | 9.0 | 154 | 5000 | 19 | 26 | 16500 |
| 3 | 2 | 99.8 | 109 | 3.19 | 3.40 | 10.0 | 102 | 5500 | 24 | 30 | 13950 |
| 4 | 2 | 99.4 | 136 | 3.19 | 3.40 | 8.0 | 115 | 5500 | 18 | 22 | 17450 |